Приложение 6. Квантили распределения Кохрена * для р = 0.05. k f

Квантили распределения Кохрена 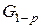^* для р = 0.05.

k	f
										¥
¥

^* Все квантили G _1-p меньше единицы, поэтому в таблице приведены лишь десятичные знаки, следующие после запятой, перед которой при пользовании таблицей нужно ставить ноль целых. Например, при n = 6, f = 3 имеем G _0.95 = 0.5321.

Приложение 7

Значения u (u¢) для различных уровней значимости.

Число степеней свободы f	Уровни значимости р		Число степеней свободы f	Уровни значимости р
0.10	0.05	0.01		0.10	0.05	0.01
	1.406	1.412	1.414			2.297	2.461	2.759
	1.645	1.689	1.723			2.326	2.493	2.800
	1.791	1.869	1.955			2.354	2.523	2.837
	1.894	1.996	2.130			2.380	2.551	2.871
	1.974	2.093	2.265			2.404	2.577	2.903
	2.041	2.172	2.374			2.426	2.600	2.932
	2.097	2.237	2.464			2.447	2.623	2.959
	2.146	2.294	2.540			2.467	2.644	2.984
	2.190	2.343	2.606			2.486	2.664	3.008
	2.229	2.387	2.663			2.504	2.683	3.030
	2.264	2.426	2.714			2.520	2.701	3.051

Приложение 8

Квантили распределения Колмогорова.

p	l1- р		p	l1- р		p	l1- р
0.99	0.44		0.50	0.83		0.15	1.14
0.90	0.57		0.40	0.89		0.10	1.22
0.80	0.64		0.30	0.97		0.05	1.36
0.70	0.71		0.25	1.02		0.02	1.52
0.60	0.77		0.20	1.07		0.01	1.63

СОДЕРЖАНИЕ

ВВЕДЕНИЕ ………………………………………………………..
ЛЕКЦИЯ 1 …………………………………………………………
1.1. Случайные величины. Классификация ошибок измерений. Абсолютная и относительная погрешность. …………..
1.2. Оценка погрешностей функций приближенных аргументов. …………………………………………………………
1.3. Распределение случайных величин. Функция распределенияи плотность распределения случайной величины...
ЛЕКЦИЯ 2 …………………………………………………………
2.1. Числовые характеристики случайной величины.Свойства математического ожидания и дисперсии.Нормированная случайная величина. ………………………………….
2.2. Нормальное и стандартное распределения случайной величины. Функция Лапласа.Задача об абсолютном отклонении. …………………………………………………………..
ЛЕКЦИЯ 3 …………………………………………………………
3.1. Генеральная совокупность и случайная выборка. Выборочная функция распределения. Гистограммы. Понятие об оценках параметров генерального распределения. ……...
3.2. Метод максимального правдоподобия. …………………
3.3. Оценка математического ожидания и дисперсии нормально распределенной случайной величины. Дисперсия среднего серии измерений. …………………………………...
ЛЕКЦИЯ 4 …………………………………………………………
4.1. Доверительные интервалы и доверительная вероятность, уровень значимости. …………………………………..
4.2. Проверка статистических гипотез, критерии значимости,ошибки первого и второго рода. ………………………..
4.3. Построение доверительного интервала для математического ожидания непосредственно измеряемой величины. Распределение Стъюдента. …………………………………...
ЛЕКЦИЯ 5 …………………………………………………………
5.1. Оценка случайной и суммарной ошибки косвенных измерений. ……………………………………………………..
5.2. Оценка дисперсии нормально распределеннойслучайной величины. …………………………………………………
5.3. Сравнение двух дисперсий. Распределение Фишера. ….
ЛЕКЦИЯ 6 …………………………………………………………
6.1. Определение дисперсии по текущим измерениям. Сравнение нескольких дисперсий. …………………………..
6.2. Сравнение двух средних. Расчет средневзвешенного значения. ………………………………………………………
6.3. Проверка однородности результатов измерений. ……..
6.4. Сравнение выборочного распределения и распределения генеральной совокупности. Критерии согласия Пирсона и Колмогорова. …………………………………………….
ПРИЛОЖЕНИЯ …………………………………………………...
Приложение 1 …………………………………………………
Приложение 2 …………………………………………………
Приложение 3 …………………………………………………
Приложение 4 …………………………………………………
Приложение 5 …………………………………………………
Приложение 6 …………………………………………………
Приложение 7 …………………………………………………
Приложение 8 …………………………………………………