Аффинные преобразования и их свойства

Линейные операторы, преобразующие плоскость саму в себя (то есть линейные операторы вида ) и имеющие обратный оператор, играют роль и потому выделяются в специальный класс.

Определение. Линейный оператор

отображающий плоскость P саму на себя, с матрицей , для которой в любом базисе , называется аффинным преобразованием плоскости.

Теорема 11.8 Если для линейного преобразования плоскости в некоторой декартовой системе координат, то это условие будет выполнено и в любой другой декартовой системе координат.

Доказательство.

Поскольку определитель произведения матриц равен произведению определителей сомножителей, то в силу теоремы 11.7 и невырожденности матрицы перехода имеем

т. е. определитель матрицы линейного преобразования плоскости не зависит от базиса. Поэтому для аффинности линейного преобразования достаточно, чтобы хотя бы в одном базисе.

Теорема доказана.

Теорема 11.9 Каждое аффинное преобразование имеет единственное обратное, которое также является аффинным.

Доказательство.

Поскольку , то матрица 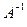существует, единственна и невырожденная, а потому система линейных уравнений

всегда имеет единственное решение для любого вектора . Но это означает, что между образами и прообразами аффинного преобразования существует взаимно однозначное соответствие, то есть для 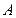существует единственное обратное аффинное преобразование, задаваемое формулами

, где .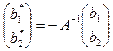

Теорема доказана.

Теорема 11.10 При аффинном преобразовании всякий базис переходит в базис, а для любых двух базисов существует единственное аффинное преобразование, переводящее первый базис во второй.

Рассмотрим теперь вопрос о том, что происходит с различными геометрическими объектами на плоскости при ее аффинном преобразовании.

Теорема 11.11 При аффинном преобразовании образом прямой линии является прямая.

Теорема 11.12 При аффинном преобразовании образом параллельных прямых являются параллельные прямые, общая точка пересекающихся прямых-прообразов переходит в точку пересечения их образов.

Теорема 11.13 При аффинном преобразовании сохраняется деление отрезка в данном отношении.

Теорема 11.14 Для всякого аффинного преобразования существует пара взаимно ортогональных направлений, которые переводятся данным аффинным преобразованием во взаимно ортогональные.