Устойчивость линейных однородных дифференциальных систем

Пусть дана однородная ЛДС (2). A(t) матрица состоящая из непрерывных функций. Покажем, что устойчивость системы (2) эквивалентна ограниченности всех его решений.

Теорема. Однородная ЛДС (2) устойчива по Ляпунову тогда и только тогда, когда каждое решение будет ограничено на полуоси .

Следствие. Если неоднородная ЛДС (1) устойчива, то все ее решения или ограничены или не ограничены при .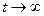

Теорема. Однородная ЛДС (2) асимптотически устойчива тогда и только тогда, когда все ее решения ® 0 при .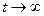

Следствие.Асимптотически устойчивая ЛДС (2) или (1) асимптотически устойчива в целом.

Устойчивость линейных дифференциальных систем с постоянной матрицей.

Пусть (1)

где А квадратная матрица (nxn) с постоянными коэффициентами. Будем искать решение в виде . Подставим это решение в систему (1).

(2)

- константа

Т.е. решение системы (1) с постоянной матрицей А ищется в виде (3)

где С – константа.

Пусть заданы начальные условия , тогда подставив их в (3) получим (4)

Пусть собственные значения матрицы А, m£n. Т.е. определена клетка Жордана и собственные вектора соответствующие . Пусть S – матрица преобразований, тогда:

J_i – соответствующие клетки Жордана.

Тогда в соответствие с (4) решение системы (1) выглядит так:

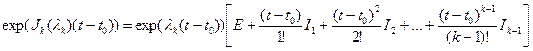
I_j – единичная матрица с поднятой на j диагональю.

Теорема. Линейная однородная система (1) с постоянной матрицей А устойчива тогда и только тогда, когда все собственные значения матрицы А имеют не положительные вещественные части., при чем собственным значениям, имеющим нулевую вещественную часть соответствуют только простые элементарные делители, т.е. соответствует единичная Жорданова клетка.

Доказательство:

Ü Пусть нам даны собственные значения 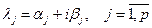(р – кратность) причем . И (q – кратность), у которых действительная часть нулевая. Т.е. общее максимально число клеток Жордана для А: m=p+q. Тогда, если мы используем (5), то решение можно записать в виде:

(6)

- полиномиальные векторы. - векторы постоянных.

Покажем что (6) ограничено. Т.к. , , 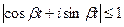а имеют ограниченную степень, которая ниже кратности собственного значения , то при 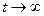. - ограниченные константы. Т.о. | y(t) |< M, где М константа. Т.е. решение ограничено и следовательно устойчиво, а значит и система устойчива.

Þ Пусть (1) устойчива. Покажем, что все собственные значения матрицы А имеют неположительные вещественные части.

Докажем от противного. Пусть существует такое собственное значение 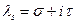при чем >0. Система (1) однородная и следовательно мы можем выписать частное решение соответствующее : . Оценим норму : 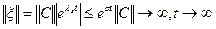. Значит, решение будет неограниченно, что противоречит условию устойчивости, тогда мы получаем, что .

Покажем, что каждое собственное значение с нулевой действительной частью имеет только простой элементарный делитель. Предположим, что А приведена к Жордановой нормальной форме, т.е. , . И некоторому с нулевой действительной частью соответствует жорданова клетка размерности l_s >1, тогда соответствующее частное решение можно выписать в виде:

(7)

матричное решение системы (1).

Подставим это решение в систему (1) и получим тождество. Домножим (7) на S и S^-1 и получим:

, т.к. это тоже решение (1), найдем его норму:

Пусть , тогда с другой стороны:

(8)

Воспользуемся (8) и получим:

(9)

Знаменатель ограничен, следовательно при 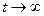выражение (9) тоже 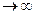, что невозможно для устойчивого решения. Т.о. мы получаем, что собственные значения, у которых действительная часть равна 0 имеют только простые элементарные делители. g

Замечание. Устойчивая линейная однородная система с постоянной матрицей А равномерно устойчива относительно начального момента t₀.

Теорема. Линейная однородная система (1) с постоянной матрицей А асимптотически устойчива тогда и только тогда, когда все собственные значения матрицы А имеют отрицательные вещественные части.