Примеры исследования на линейную зависимость систем векторов

Пример 1.1. Исследовать на линейную зависимость и найти ранг системы многочленов :

, ,

, .

В случае линейной зависимости найти подсистему , являющуюся линейно независимой. Выразить векторы через векторы подсистемы .

Решение. Составим равенство (1.2):

.

Запишем систему вида (1.5) с основной матрицей :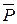

.

После приведения матрицы 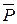к ступенчатому виду при помощи метода Жордана-Гаусса (в результате элементарных преобразований нумерация столбцов осталась прежней), получим

.

Перейдем от ступенчатой матрицы к системе уравнений. Получим

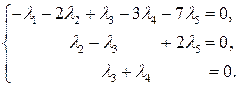
Так как , то выберем за базисные (основные) переменные , за свободные – переменные . Выражая базисные переменные через свободные, получим общее решение ОСЛАУ

Так как , то , следовательно, рассматриваемая система многочленов линейно зависима. В качестве линейно независимой подсистемы примем . Тогда остальные векторы можно выразить через векторы подсистемы . Положив , получим 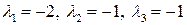. Тогда из равенства (1.2) следует, что

.

Аналогично взяв , получим и

.