 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Магнитное поле в веществе)
|
|
Магнитное поле в веществе. При изучении магнитного поля в веществе различают два типа токов – макротоки и микротоки. Макротоками называются токи проводимости и конвекционные токи, связанные с движением заряженных макроскопических тел. Микротоками (молекулярными токами) называют токи, обусловленные движением электронов в атомах, молекулах и ионах. Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками и внутреннего или собственного, магнитного поля, создаваемого микротоками.
Ампер выдвинул следующую гипотезу: в веществе циркулируют замкнутые токи. Каждый замкнутый
ток представляет собой магнитный момент и создает магнитное поле вокруг себя. Без внешнего поля в
обычных средах (не ферромагнитных) они ориентированы беспорядочно и полное поле от них равно нулю.
Под влиянием внешнего магнитного поля магнитные моменты молекул приобретают преимущественную
ориентацию. Отсюда суммарный магнитный момент образца не равен нулю, вещество – магнетик,
намагничивается и в нем появляется внутреннее магнитное поле B
| Магнитное поле в веществе |
При изучении магнитного поля в веществе различают два типа токов – макротоки и микротоки. Макротоками называются токи проводимости и конвекционные токи, связанные с движением заряженных макроскопических тел. Микротоками (молекулярными токами) называют токи, обусловленные движением электронов в атомах, молекулах и ионах. Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками и внутреннего, или собственного, магнитного поля, создаваемого микротоками. Характеризует магнитное поле в веществе вектор
Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность
где Для того чтобы связать вектор намагниченности среды
а б в Каждый атомный ток в плоскости сечения стержня, перпендикулярной его оси, представляет микроскопический кружок, причем все микротоки текут в одном направлении – против часовой стрелки (рис. 6.3, б). В местах соприкосновения отдельных атомов и молекул (А, В) молекулярные токи противоположно направлены и компенсируют друг друга (рис.6.3, в). Нескомпенсированными остаются лишь токи, текущие вблизи поверхности материала, создавая на поверхности материала некоторый микроток Закон полного тока для магнитного поля в вакууме можно обобщить на случай магнитного поля в веществе:
где Как видно из рисунка 6.4, вклад в
Рис. 6.4 Алгебраическая сумма сил микротоков связана с циркуляцией вектора намагниченности соотношением
тогда закон полного тока можно записать в виде
Вектор
называется напряженностью магнитного поля. Таким образом, закон полного тока для магнитного поля в веществе утверждает, что циркуляция вектора напряженности магнитного поля
Выражение (6.3.6) – это закон полного тока в интегральной форме. В дифференциальной форме его можно записать:
Намагниченность изотропной среды с напряженностью
где |
Дата публикования: 2015-07-22; Прочитано: 1368 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!

 , равный геометрической сумме
, равный геометрической сумме  и
и  магнитных полей:
магнитных полей: ,
,
 , равная отношению магнитного момента малого объема вещества к величине этого объема:
, равная отношению магнитного момента малого объема вещества к величине этого объема: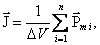 ,
,
 – магнитный момент i -го атома из числа n атомов, в объеме Δ V.
– магнитный момент i -го атома из числа n атомов, в объеме Δ V.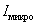 , рассмотрим равномерно намагниченный параллельно оси цилиндрический стержень длиной h и поперечным сечением S (рис. 6.3, а). Равномерная намагниченность означает, что плотность атомных циркулирующих токов внутри материала
, рассмотрим равномерно намагниченный параллельно оси цилиндрический стержень длиной h и поперечным сечением S (рис. 6.3, а). Равномерная намагниченность означает, что плотность атомных циркулирующих токов внутри материала 

 ,
,
 – алгебраическая сумма макро- и микротоков сквозь поверхность, натянутую на замкнутый контур L.
– алгебраическая сумма макро- и микротоков сквозь поверхность, натянутую на замкнутый контур L.
 ,
,
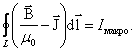 ,
,

 вдоль произвольного замкнутого контура L равна алгебраической сумме макротоков сквозь поверхность, натянутую на этот контур:
вдоль произвольного замкнутого контура L равна алгебраической сумме макротоков сквозь поверхность, натянутую на этот контур: ,
,
 ,
,
 ,
,
 – коэффициент пропорциональности, характеризующий магнитные свойства вещества и называемый магнитной восприимчивостью среды. Он связан с магнитной проницаемостью соотношением
– коэффициент пропорциональности, характеризующий магнитные свойства вещества и называемый магнитной восприимчивостью среды. Он связан с магнитной проницаемостью соотношением  .
.