для студентов экономических специальностей 4 страница

Пример. Найти решение задачи целочисленного линейного программирования:

- целые

В результате решения данной задачи симплексным методом без условия целочисленности получили симплекс-таблицу, соответствующую оптимальному решению (см. Таб.3.) и оптимальное решение при .

Поскольку среди компонент оптимального решения есть нецелые ( и ), то для нахождения целочисленного оптимального решения среди нецелых компонент выбирается компонента с наибольшей дробной частью, и по соответствующей строке в симплекс-таблице формируется правильное отсечение.

Наибольшую дробную часть имеет , т.к.

.

Поэтому сформируем правильное отсечение - неравенство по строке, соответствующей этой компоненте.

Это неравенство введением дополнительной неотрицательной целочисленной переменной преобразуем в равносильное уравнение:

Полученное соотношение добавляем в симплекс-таблицу дополнительной строкой (свободный член вносим без изменения знака, а коэффициенты при свободных переменных - с противоположным знаком).

Базисные переменные	Свободные члены	Свободные переменные
x4	x5
x1
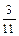
x3
x2
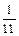
x6
Z

Полученную расширенную задачу решаем симплекс-методом.

Базисное решение - недопустимое, т.к. имеется отрицательный элемент, ограничения совместны (в строке, имеющей отрицательный свободный член есть отрицательные элементы).

Столбец, соответствующий , принимаем в качестве разрешающего. Для определения разрешающей строки найдем минимальное положительное отношение свободных членов к элементам разрешающего столбца: .

Базисную переменную переводим в свободные переменные, а свободную переменную - в базисные.

В результате преобразования симплекс-таблицы получим:

Базисные переменные	Свободные члены	Свободные переменные
x6	x5
x1			-3
x3			-8
x2			-1
x4		-11	9
Z			-19

Базисное решение - допустимое, т.к. в столбце свободных членов нет ни одного отрицательного элемента, но неоптимальное (в строке целевой функции, кроме столбца свободных членов, элементы не одного знака). Целевая функция ограничена сверху, т.к. в столбце, не удовлетворяющем признаку оптимальности, есть положительные элементы.

Столбец, не удовлетворяющий признаку оптимальности (), принимаем в качестве разрешающего. Разрешающей является строка , т.к. .

Базисную переменную переводим в свободные переменные, а свободную переменную - в базисные.

Преобразуем симплекс-таблицу:

Базисные переменные	Свободные члены	Свободные переменные
x6	x4
x1
x3
x2
x5
Z

Базисное решение - допустимое, т.к. в столбце свободных членов нет ни одного отрицательного элемента, и оптимальное (в строке целевой функции все элементы положительные (одного знака)).

Найденное оптимальное решение целочисленное, следовательно, задача целочисленного программирования решена.

Максимальное значение целевой функции при .

9. Транспортная задача

Постановка транспортной задачи.

У m поставщиков сосредоточен однородный груз в количествах соответственно . Имеющийся груз необходимо доставить n потребителям , спрос которых равен соответственно . Известна стоимость перевозки единицы груза от i – го поставщика к j - му потребителю - . Требуется найти оптимальный план перевозок, обеспечивающий минимальные затраты и вывоз грузов и удовлетворение потребностей.

Экономико-математическая модель задачи.

Пусть - количество единиц груза, которое необходимо доставить от i – го поставщика к j - му потребителю.

Целевая функция:

(1)- минимизация общих затрат на реализацию плана перевозок.

Ограничения на запасы поставщиков:

(2) - все запасы должны быть вывезены.

Ограничения на спрос потребителей:

(3) - все потребности должны быть удовлетворены.

Условия неотрицательности:

(4)

Модель транспортной задачи называют закрытой, если суммарный объём груза, имеющегося у поставщиков, равен суммарному спросу потребителей, т.е. выполняется условие . Если это условие не выполняется (), то модель транспортной задач называется открытой.

Если , то открытая транспортная задача сводится к закрытой путем ведения фиктивного потребителя с объемом потребностей и стоимостями перевозок, равными нулю. Если , то вводится фиктивный поставщик с объемом груза и стоимостями перевозок, равными нулю.

Число переменных в транспортной задаче с m поставщиками и n потребителями равно nm, а число уравнений в системах (2) и (3) равно n+m. Так как предполагается, что выполняется условие , то число линейных независимых уравнений равно n+m-1. Следовательно, опорный план транспортной задачи может иметь не более n+m-1 отличных от нуля неизвестных.

Если в опорном плане число отличных от нуля компонент равно n+m-1, то план является невырожденным, а если меньше – то вырожденным.

Транспортная задача является канонической задачей линейного программирования, и для ее решения в принципе можно использовать симплекс-метод. Однако, в силу специфичности транспортной задачи, используются более эффективные методы.

Алгоритм решения транспортной задачи (методом потенциалов).

1. Определяется исходный план (метод северо-западного угла, метод минимальной стоимости и др.).

2. Производится оценка плана.

3. Осуществляется переход к следующему плану.

Получение исходного плана основано на заполнении следующей таблицы:

		……		……
		……		……
……	……	……	…….	……	……
		……		……
……	……	……	………	……	……
		……		……

В каждой ячейке в левом верхнем углу помещаются стоимости перевозок, в правом нижнем углу объемы поставок от i -го поставщика к j- му потребителю. В верхней строке указываются мощности поставщиков, в левом столбце – спрос потребителей.

Рассмотрим методы получения первого опорного плана.

а) Метод северо-западного угла.

Рассматривается незаполненная левая верхняя ячейка. Эта ячейка заполняется минимальным значением от возможного объема поставок и объема потребностей. В результате или будут удовлетворены все потребности, или исчерпаны запасы поставщика. Если удовлетворены потребности, то остальные ячейки этого столбца зачеркиваются и в последующих распределениях не участвуют.

Если исчерпаны запасы поставщика, то зачеркиваются остальные ячейки соответствующей строки, и они не участвуют в последующих распределениях.

Вновь рассматривается незаполненная северо-западная ячейка, и итерации повторяются.

Замечание. Этот метод не учитывает стоимость перевозок, и поэтому исходный план может оказаться далеким от оптимального.

б) Метод минимальной стоимости.

Из всех незаполненных ячеек находится ячейка с минимальной стоимостью перевозок. Эта ячейка заполняется минимальным значением от возможного объема поставок и объема потребностей. В результате или будут удовлетворены потребности, или исчерпаны запасы.

Если исчерпаны запасы, зачеркиваются остальные ячейки соответствующей строки, и они не участвуют в последующих распределениях.

Если удовлетворены все потребности, то зачеркиваются остальные ячейки соответствующего столбца, и они не участвуют в последующих распределениях.

Вновь из всех незаполненных ячеек находится ячейка с минимальной стоимостью, итерации повторяются.

Если план получается вырожденным, т.е. m+n-1 не совпадает с числом заполненных ячеек, то вводится фиктивно заполненная нулем ячейка. Для этого из всех незаполненных ячеек находится ячейка с минимальной стоимостью. Если на основе этой ячейки невозможно построить замкнутый цикл со всеми заполненными вершинами, то она принимается в качестве фиктивной. В обратном случае эта ячейка исключается из рассмотрения претендентов на фиктивную ячейку.

Для оценки плана:

1) Вычисляются потенциалы поставщиков и потребителей . Потенциалы для заполненных ячеек распределительной таблицы удовлетворяют условию (5).

Для получения решения системы уравнений (5) используется тождество .

2) Вычисляются оценки свободных ячеек

Если все , то план оптимальный. Если для всех ячеек , то оптимальный план является единственным. Если какая-либо оценка , то существует бесчисленное множество решений с одинаковым значением целевой функции (решение оптимальное, но альтернативное). Если какое-либо значение , то план неоптимальный, и необходимо произвести загрузку свободной ячейки (получение новой таблицы).

Для перехода к следующему опорному плану для ячейки с минимальной отрицательной оценкой строится замкнутый цикл с вершинами в заполненных ячейках (Замкнутый цикл – это ломаная линия (возможно, прямоугольник), вершинами которой являются заполненные ячейки, кроме одной свободной ячейки с минимальной отрицательной оценкой).

В свободную вершину цикла вписывается “+”, а все последующие вершины по часовой стрелке будут иметь “-”, “+”, “-”,…

Находится минимальный объем груза для всех отрицательных вершин цикла. В вершинах цикла со знаком «+» объем увеличивается на эту величину, в вершинах со знаком «-» - уменьшается. В результате баланс распределения не нарушается.

Затем снова производится оценка опорного плана.

Замечание: Если полученный опорный план вырожденный, то необходимо выбрать свободную ячейку с минимальной стоимостью без образования замкнутого цикла с заполненными вершинами и в эту ячейку вписать ноль.

Рассмотрим пример решения транспортной задачи.

Пример. Предприятие имеет 3 склада готовой продукции: А₁, А_2, А_3, на которых соответственно имеются 70, 90 и 60 единиц товара. Рынкам сбыта, находящимся в городах B_1, B_2, B_3, B₄, необходимо распределить следующее количество единиц продукции – 90, 40, 50 и 20. Стоимость перевозки единицы продукции со склада на рынок сбыта задается таблицей (в у.е.):

Склады	Мощность складов	Потребности рынков сбыта
B1	B2	B3	B4
А1
А2
А3

Необходимо составить план распределения товаров между рынками сбыта, обеспечивающий минимальные транспортные издержки.

Составим экономико-математическую модель данной задачи.

Обозначим через - объём перевозки от i –ого склада j – ому рынку сбыта.

Тогда суммарные затраты на перевозку Z составят:

Заданные мощности складов и потребности рынков сбыта накладывают ограничения на значения объемов перевозок :

- Мощности всех складов должны быть реализованы:

- Спросы потребителей должны быть удовлетворены:

- Объемы перевозимых грузов не могут быть отрицательными:

Решение.

1. Определим характер транспортной задачи.

Так как (суммарные мощности не равны суммарным потребностям), то данная задача является открытой и необходимо её привести к закрытой. Для этого введем фиктивного потребителя (рынок сбыта), потребность которого составляет . Все значения стоимости перевозок для этого потребителя .

После введения фиктивного потребителя задача становится закрытой, и её можно решить методом потенциалов.

2. Заполним распределительную таблицу исходными данными.

В результате введения фиктивного потребителя распределительная таблица исходных данных примет вид:

3. Составим первый опорный план методом «минимальной стоимости».

В первую очередь заполняется ячейка с минимальной стоимостью. Это ячейки с нулевой стоимостью. Сравним максимально возможные поставки для этих ячеек: для ячейки (1,5) , для ячейки (2,5) , для ячейки (3,5) . Так как для ячеек (1,5), (2,5) и (3,5) эти значения равны, то произведем максимально возможную поставку в любую из них. Например, в ячейку (1,5) даем поставку, равную 20. В результате потребность фиктивного рынка сбыта удовлетворена, и последний столбец таблицы поставок выпадает из рассмотрения.

В оставшейся таблице наименьшей стоимостью, равной 1, обладает ячейка (1,2). Поскольку на складе в наличии имеется 70-20 = 50 единиц товара, то мы можем полностью удовлетворить потребность 2-ого рынка сбыта, и 2-ой столбец выпадает из дальнейшего рассмотрения.

		1 40			0 20

Далее заполняем ячейку (1,1), т.к. она обладает наименьшей стоимостью перевозки, равной 2. Потребность 2-ого склада равна 90 единицам товара, но с 1-ого склада ранее были вывезены 40 единиц товара для 2-ого рынка сбыта и 20 единиц товара для 5-ого склада. Поэтому на 1-ый рынок сбыта мы можем поставить только 10 единиц товара, и товары, находившиеся в наличии 1-ого склада, полностью вывезены, т.е. 1-ая строка выпадает из дальнейшего рассмотрения.

	2 10	1 40			0 20

В оставшейся таблице минимальными стоимостями (равной 3) обладают ячейки (2,3) и (3,1). Потребность 3-ого рынка сбыта равна 50 единицам товара, и 2-ой склад (его мощность составляет 90 единиц товара) может полностью её удовлетворить. Потребность 1-ого рынка сбыта равна 60 единицам товара, и 1-ый склад также может полностью её удовлетворить (оставшаяся мощность равна 90 - 10=80 единиц).

Максимально возможную поставку, равную 60 единицам, произведем в ячейку (1,3), тогда последняя строка выпадает из рассмотрения.

	2 10	1 40			0 20
	3 60

Рассуждая аналогичным образом, заполним оставшуюся часть распределительной таблицы. В результате получим: