 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
для студентов экономических специальностей 1 страница
|
|
Камский Государственный Политехнический Институт
ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МОДЕЛИ и МЕТОДЫ
Линейное программирование
Учебное пособие
для студентов экономических специальностей
Набережные Челны
Учебное пособие по экономико-математическим моделям и методам разработано на кафедре «Математическое моделирование и информационные технологии в экономике» и предназначено для студентов экономических специальностей. Оно включает в себя теоретический материал, примеры моделирования реальных экономических задач и их методы решения. Приведенные алгоритмы решения задач ориентированы на использование современных информационных технологий.
Для организации самостоятельной работы приводятся варианты индивидуальных заданий с примерами их решения.
Составители: Смирнов Ю.Н., Шибанова Е.В.
Набережные Челны: Изд-во КамПИ, 2004, 81 с.
Рецензент: доцент, кандидат физико-математических наук Углов А.Н.
Печатается по решению научно-методического совета Камского государственного политехнического института от 24.03.03 г.
Камский Государственный
Политехнический Институт,
Содержание
Содержание. 3
Введение. 4
1. Примеры задач линейного программирования. 5
2. Общая, стандартная и основная задачи линейного программирования 8
3. Геометрическая интерпретация задачи линейного программирования 11
4. Графический метод решения задачи линейного программирования 13
5. Симплекс - метод решения задач линейного программирования 17
6. Двойственные задачи линейного программирования. 32
7. Двойственный симплекс-метод. 42
8. Задача целочисленного линейного программирования. 45
9. Транспортная задача. 51
10. Задачи производственного менеджмента. 69
Задание для самостоятельной работы.. 73
Варианты задач для самостоятельной работы.. 74
Литература. 81
Введение
Линейное программирование является одним из разделов математического программирования – дисциплины, занимающей изучением экстремальных задач и разработкой методов их решения.
В общем виде постановка экстремальной задачи математического программирования состоит в определении наибольшего или наименьшего значения функции  , называемой целевой функцией, при условиях
, называемой целевой функцией, при условиях  , где f и
, где f и  - заданные функции, а
- заданные функции, а  - заданные постоянные величины. При этом ограничения в виде равенств определяют множество допустимых решений, а
- заданные постоянные величины. При этом ограничения в виде равенств определяют множество допустимых решений, а  - называются проектными параметрами.
- называются проектными параметрами.
В зависимости от свойств функции f и  задачи математического программирования делятся на ряд классов задач. Далеко неполная схема задач математического программирования приведена на рис.1.
задачи математического программирования делятся на ряд классов задач. Далеко неполная схема задач математического программирования приведена на рис.1.
Среди них наиболее изученными являются задачи линейного программирования (ЛП), когда все функции f и  - линейные.
- линейные.
Нелинейное программирование – если хотя бы одна из функций f и  - нелинейная.
- нелинейная.
Выпуклое программирование – если отыскивается минимум выпуклой (максимум вогнутой) функции, заданной на выпуклом замкнутом множестве.
Целочисленное программирование – если проектные параметры могут принимать лишь целочисленные значения.
Дробно-линейное программирование – если целевая функция f – квадратичная,  - линейные.
- линейные.
Параметрическое программирование – если функции f и  зависят от некоторых параметров.
зависят от некоторых параметров.
Стохастическое программирование – если в функциях f и  содержаться случайные величины.
содержаться случайные величины.
Динамическое программирование – если процесс нахождения решения является многоэтапным.
Рассмотрим задачи, сводящиеся к задачам линейного программирования.

1. Примеры задач линейного программирования
Задача использования ресурсов.
Для производства n видов продукции предприятие использует m видов ресурсов (сырья). Известны нормы затрат ресурсов для производства единицы продукции каждого вида: 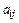 - норма затрат i – ого ресурса для производства единицы продукции j – ого вида.
- норма затрат i – ого ресурса для производства единицы продукции j – ого вида.
Ресурсы предприятия имеются в ограниченных объемах  . Предположим, прибыль (доход) от реализации единицы продукции каждого вида величина известная, равная
. Предположим, прибыль (доход) от реализации единицы продукции каждого вида величина известная, равная  .
.
Необходимо при заданных ограничениях на ресурсы определить оптимальный план производства каждого вида продукции, обеспечивающий максимум прибыли.
Обозначим через  план производства каждого вида продукции.
план производства каждого вида продукции.
Найти максимальное значение линейной функции цели (прибыли или дохода) 
при линейных ограничениях
 (ограничения на ресурсы);
(ограничения на ресурсы);
 (условие неотрицательности плана производства).
(условие неотрицательности плана производства).
Ниже будет показано, что эта задача нахождения оптимального плана есть стандартная задача линейного программирования.
Замечания:
1. Величины  должны быть определены на основе маркетинговых исследований цен на продукцию и анализа себестоимости единицы продукции.
должны быть определены на основе маркетинговых исследований цен на продукцию и анализа себестоимости единицы продукции.
2. В модели не учтены емкость рынка и объем поступивших заказов. Учет этих факторов рынка можно записать в виде ограничений  , где
, где  соответственно объем заказов и предельная емкость рынка
соответственно объем заказов и предельная емкость рынка  - ой продукции. Это свидетельство взаимосвязанности задач маркетинга и планирования производства.
- ой продукции. Это свидетельство взаимосвязанности задач маркетинга и планирования производства.
3. Оптимальный объем и номенклатура производства могут определяться не только первоначальными запасами ресурсов  , но и объемом выделенных финансов на производство
, но и объемом выделенных финансов на производство  . Тогда ограничения на ресурсы и финансы запишутся в виде следующих неравенств
. Тогда ограничения на ресурсы и финансы запишутся в виде следующих неравенств

где  - цены на ресурсы, определяемые также из маркетинговых исследований,
- цены на ресурсы, определяемые также из маркетинговых исследований,  - искомые объемы закупаемых ресурсов.
- искомые объемы закупаемых ресурсов.
Таким образом, процесс математического моделирования реальных задач сводится к все большему учету реальных факторов. Эти факторы оказываются связывающими различные деловые процессы предприятия. В нашем случае оказались связанными задачи таких деловых процессов, как, ПРОИЗВОДСТВО, МАРКЕТИНГ, МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ, СБЫТ, ФИНАНСЫ.
Банковская задача
Свободные средства банка могут быть направлены на выдачу кредитов и приобретение ценных бумаг. Если предположить, что выданные кредиты не являются в полном смысле ликвидными, а ценные бумаги ликвидные, и в то же время кредиты приносят банку больший доход, чем ценные бумаги, то можно поставить задачу определения оптимального плана использования свободных средств.
Предположим, банк имеет свободных средств в размере 120 млн. рублей. Выданные кредиты или обязательства банка по кредитам составляют не менее 30 млн. рублей. Исходя из стратегии (безопасности) банка, не менее чем 40% всех используемых средств должны находиться в ценных бумагах (в ликвидных ресурсах, для выполнения возможных непрогнозируемых обязательств). Определить оптимальный план использования средств, если доход от выданных кредитов составляет в среднем - 20%, а от ценных бумаг – 10%.
Экономико-математическая модель задачи:
Предположим, 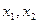 средства банка размещенные соответственно в кредитах и ценных бумагах. Тогда получим следующую задач линейного программирования:
средства банка размещенные соответственно в кредитах и ценных бумагах. Тогда получим следующую задач линейного программирования:
Найти максимум линейной целевой функции – функции дохода

при заданных ограничениях по свободным средствам, по объему выдаваемых кредитов и по стратегии банка

Таким образом, задача определения стратегии банка так же, как и задача использования ресурсов, сводится к стандартной задаче линейного программирования.
2. Общая, стандартная и основная задачи линейного программирования
Определение 1. Общей задачей ЛП называется задача нахождения максимального (минимального) значения линейной целевой функции
 (1) при условиях
(1) при условиях
 ,
,  (2)
(2)
 ,
, 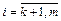 (3)
(3)
 ,
, 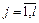 ,
,  (4),
(4),
где  ,
,  ,
,  - заданные постоянные величины и
- заданные постоянные величины и  .
.
Определение.2. Функция Z называется целевой функцией задачи (1 - 4),  - проектными параметрами задачи, а условия (2 - 4) ограничениями данной задачи.
- проектными параметрами задачи, а условия (2 - 4) ограничениями данной задачи.
Определение 3. Стандартной задачей ЛП называется задача нахождения целевой функции (1) при выполнении условий (2), (4), где k=m, l=n, т.е. когда ограничения заданы только в виде неравенств (2), и все проектные параметры удовлетворяют условиям неотрицательности (4), а условия в виде равенств отсутствуют:

 ,
, 
 ,
,  .
.
Определение 4. Канонической (или основной) задачей ЛП называется задача нахождения максимального (минимального) значения функции (1) при выполнении условий (3), (4), где k=0,l=n, m<n,т.е. когда ограничения заданы только в виде равенств (3), и все проектные параметры удовлетворяют условиям неотрицательности (4), а условия в виде неравенств (2) отсутствуют:

 ,
, 
 ,
,  ,
,  .
.
Определение 5. Совокупность значений проектных параметров  , удовлетворяющих ограничениям задачи (2-4), называется допустимым решением, или планом.
, удовлетворяющих ограничениям задачи (2-4), называется допустимым решением, или планом.
Определение 6. План  , при котором целевая функция (1) принимает свое максимальное (минимальное) значение, называется оптимальным, т.е.
, при котором целевая функция (1) принимает свое максимальное (минимальное) значение, называется оптимальным, т.е.  .
.
Все три формы задачи ЛП эквивалентны, ибо каждая из них с помощью некоторых преобразований может быть переписана в форме другой задачи. При этом необходимо пользоваться следующими правилами:
1. Задачу минимизации функции можно свести к задаче максимизации, и, наоборот, путем замены знаков коэффициентов  на противоположные, поскольку
на противоположные, поскольку  .
.
2. Ограничения-неравенства (2) можно заменить эквивалентными ограничениями-равенствами путем введения дополнительных неотрицательных переменных следующим образом:
Ограничение-неравенство вида  преобразуется в ограничение-равенство
преобразуется в ограничение-равенство  ,
,  , а ограничение-неравенство вида
, а ограничение-неравенство вида  - в ограничение-равенство
- в ограничение-равенство  ,
,  .
.
При этом число дополнительных переменных равно числу преобразуемых неравенств.
Вводимые дополнительные переменные имеют вполне определенный смысл. Так, например, для задачи распределения ресурсов числовое значение дополнительной переменной равно объему неиспользованного соответствующего ресурса. С математической точки зрения основные и дополнительные переменные играют одинаковую роль. Поэтому целесообразно их единообразное обозначение.
4. Каждое ограничение-равенство вида (3) можно записать в виде двух неравенств  .
.
5. Переменная  , неограниченная условием неотрицательности вида (4), можно заменить разностью двух дополнительных неотрицательных переменных:
, неограниченная условием неотрицательности вида (4), можно заменить разностью двух дополнительных неотрицательных переменных:  ,
,  ,
,  .
.
3. Геометрическая интерпретация задачи линейного программирования
Рассмотрим задачу, состоящую в определении максимального значения функции:
 (5) при условиях
(5) при условиях
 ,
,  (6)
(6)
 ,
,  (7).
(7).
Эта задача ЛП в стандартной форме с двумя переменными.
Каждое неравенство вида (6), (7) геометрически определяет полуплоскость соответственно с граничными прямыми
 (8).
(8).
При этом вектор  , как градиента функции
, как градиента функции  , указывает ту полуплоскость, которая определяется неравенством
, указывает ту полуплоскость, которая определяется неравенством  , а вектор
, а вектор  - полуплоскость, определяемую неравенством
- полуплоскость, определяемую неравенством  .
.
Если система неравенств (6), (7) совместна, то область её решений есть множество точек, принадлежащих всем указанным полуплоскостям. Пересечение этих полуплоскостей образует выпуклый многоугольник решений, или область допустимых решений (ОДР).
Таким образом, исходная задача ЛП состоит в нахождении таких точек многоугольника решений, в которых целевая функция Z принимает максимальное (минимальное) значение. Эта точка существует тогда, когда многоугольник решений не пуст, и на нем целевая функция ограничена.
Линейная целевая функция достигает точек экстремума только на границе выпуклого многоугольника.
Рассмотрим градиент функции цели  . Это будет вектор
. Это будет вектор  (см. рис.2.), указывающий направление возрастания функции цели. Очевидно, если взять обратное направление, то это будет направлением убывания функции цели. Если построить произвольную прямую
(см. рис.2.), указывающий направление возрастания функции цели. Очевидно, если взять обратное направление, то это будет направлением убывания функции цели. Если построить произвольную прямую  - const, то её движение параллельно самой себе в направлении вектора
- const, то её движение параллельно самой себе в направлении вектора  приведет к возрастанию функции цели. При этом для допустимости решения эта прямая должна иметь хотя бы одну общую точку с многоугольником решений. Два крайних положения этой прямой в ОДР соответствуют наименьшему и наибольшему значениям целевой функции. При этом могут встретиться случаи, изображенные на рис.2-5, когда исходная задача имеет единственное решение (минимальное и максимальное значение) (рис.2), множество решений (координаты любой точки прямой
приведет к возрастанию функции цели. При этом для допустимости решения эта прямая должна иметь хотя бы одну общую точку с многоугольником решений. Два крайних положения этой прямой в ОДР соответствуют наименьшему и наибольшему значениям целевой функции. При этом могут встретиться случаи, изображенные на рис.2-5, когда исходная задача имеет единственное решение (минимальное и максимальное значение) (рис.2), множество решений (координаты любой точки прямой  на рис.3), и решение исходной задачи не существует в силу неограниченности целевой функции (рис.4) или несовместности системы неравенств (6), (7) (рис.5).
на рис.3), и решение исходной задачи не существует в силу неограниченности целевой функции (рис.4) или несовместности системы неравенств (6), (7) (рис.5).
 |
4. Графический метод решения задачи линейного программирования
Графическим методом решается стандартная задача линейного программирования:

 ,
, 
 ,
,  .
.
Данный метод основан на приведенной выше геометрической интерпретации задачи ЛП. Нахождение решения задачи ЛП графическим методом имеет следующие этапы:
1. Строят прямые (8), уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.
2. Находят полуплоскости, определяемые каждым из ограничений задачи.
3. Находят многоугольник решений как пересечение всех полуплоскостей
4. Строят начальную прямую (линию уровня целевой функции), проходящую через начало координат  .
.
5. Строят вектор  , представляемый градиент целевой функции (5).
, представляемый градиент целевой функции (5).
6. Движением прямой  - const параллельно самой себе в направлении вектора
- const параллельно самой себе в направлении вектора  либо находят точки, в которой целевая функция принимает наибольшее (наименьшее) значение, либо устанавливают неограниченность сверху (снизу) целевой функции на множестве планов.
либо находят точки, в которой целевая функция принимает наибольшее (наименьшее) значение, либо устанавливают неограниченность сверху (снизу) целевой функции на множестве планов.
7. Определяют координаты точки максимума (минимума) целевой функции и вычисляют ее значение в этих точках.
Пример. Найти наибольшее и наименьшее значения целевой функции z при заданных ограничениях:

1. Строят прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств:
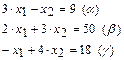
2. Каждое ограничение-неравенство определяет координатную полуплоскость. В зависимости от знака неравенств при помощи двух стрелок укажем требуемые полуплоскости.
3. В результате пересечения всех полуплоскостей находят многоугольник решений (на рисунке обозначен треугольником ABC).
4. Построим начальную прямую (линию уровня целевой функции), проходящую через начало координат  .
.
5. Движением прямой  параллельно самой себе в направлении вектора
параллельно самой себе в направлении вектора  находим два крайних положения. Первое соответствует минимуму целевой функции (точка А), второе - максимуму (точка С).
находим два крайних положения. Первое соответствует минимуму целевой функции (точка А), второе - максимуму (точка С).
Рис.6. Графическая интерпретация задачи линейного программирования

6. Определим координаты точек максимума и минимума целевой функции и вычислим их значения в найденных точках.
- Точка минимума лежит на пересечении прямых  и
и 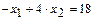 :
: 
- Точка максимума лежит на пересечении прямых  и
и 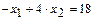 :
: 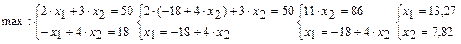 Минимальное значение целевой функции
Минимальное значение целевой функции  .
.
Максимальное значение целевой функции  .
.
Вообще, с помощью графического метода может быть решена задача ЛП, система ограничений которой содержит n неизвестных и m линейно-независимых уравнений, если n и m связаны соотношением  .
.
Действительно, пусть поставлена каноническая задача ЛП: найти наибольшее значение
 (12) при условиях
(12) при условиях
 ,
,  (13),
(13),
 ,
,  (14),
(14),
где все уравнения (13) линейно независимы, и выполняется соотношение  .
.
Используя метод Жордана-Гаусса, производим m исключений, в результате которых система ограничений примет вид:
 ,
, 
 ,
,  . (15)
. (15)
Учитывая неравенства (14), эту систему уравнений можно записать в виде системы неравенств  ,
,  ,
,  ,
,  . Исключая
. Исключая  из (12) при помощи уравнений (15), получим
из (12) при помощи уравнений (15), получим  , т.е. задачу вида (5-7).
, т.е. задачу вида (5-7).
5. Симплекс - метод решения задач линейного программирования
Введение.
Предположим, что поставлена стандартная задача ЛП:
 ,
,
 ,
,  , (16)
, (16)
 ,
,  .
.
Каждое из условий типа неравенства определяет полупространство, ограниченное гиперплоскостью (плоскостью в k -мерном пространстве). Пересечение соответствующих полупространств образует выпуклый многогранник (область допустимых решений - ОДР), в котором необходимо найти максимум (минимум) целевой функции. Внутри многогранника условий в силу его выпуклости линейная функция z не может достигать максимума (минимума). Её максимум (минимум), если он существует, достигается обязательно в какой-нибудь вершине многогранника или на одном из его граней.
Теоретически задача ЛП проста. Достаточно найти конечное число вершин многогранника и вычислить в них значения целевой функции. Из всех этих значений выбрать то, которое соответствует оптимальному решению.
Дата публикования: 2015-07-22; Прочитано: 1300 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
