для студентов экономических специальностей 3 страница

В качестве разрешающего столбца выбираем столбец . Вычисляя , получаем, что в качестве разрешающей строки следует выбрать . Базисную переменную переводим в свободные, а свободную переменную - в базисные.

В результате преобразования симплекс-таблицы получили следующую таблицу:

Базисные переменные	Свободные члены	Свободные переменные
x3	x5
x1
x4			1
x2
Z

Базисное решение - допустимое, т.к. все свободные члены положительные. Решение оптимальное (минимум целевой функции), поскольку в строке целевой функции, кроме столбца свободных членов, все элементы одного знака (отрицательные). Оптимальное решение единственное, т.к. в строке целевой функции нет нулевых элементов. Данная симплекс-таблица соответствует точке А на рис.6.

Но поскольку требуется найти максимальное значение целевой функции, то итерации продолжаются.

В качестве разрешающего столбца можно выбрать любой столбец таблицы, т.к. они оба не удовлетворяют признаку оптимальности (максимуму). Выбираем столбец . Тогда разрешающей строкой будет строка , т.к. .

В результате преобразований получим следующую симплекс-таблицу:

Таб.3. Симплекс-таблица оптимального решения

Базисные переменные	Свободные члены	Свободные переменные
x4	x5
x1
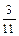
x3
x2
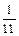
Z

Базисное решение - допустимое, т.к. все свободные члены положительные. Решение оптимальное (максимум целевой функции), поскольку в строке целевой функции все элементы одного знака (положительные). Оптимальное решение единственное, т.к. в строке целевой функции нет нулевых элементов. Данная симплекс-таблица соответствует точке С на рис.6.

Таким образом, наибольшее значение целевая функция имеет при .

6. Двойственные задачи линейного программирования

Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу, называемую двойственной или сопряженной по отношению к исходной или прямой.

1. Симметричная пара взаимно двойственных задач:

Рассматривается стандартная задача линейного программирования (СЗЛП):

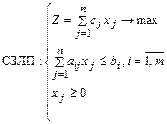
Тогда двойственная ей задача (ДЗЛП) будет иметь вид:

Экономическая интерпретация взаимно двойственных задач.

СЗЛП: Составить такой план продукции 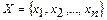, при котором выручка (прибыль) от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющиеся запасы.

ДЗЛП: Найти такой набор цен (оценок) ресурсов , при которых общие затраты на ресурсы будут минимальными, а созданная стоимость единицы продукции каждого вида будет не менее выручки от реализации единицы продукции. Оценки называются учетными или теневыми.

Положительную двойственную оценку имеют лишь те виды ресурсов, которые полностью используются при оптимальном плане производства продукции и увеличить этот доход можно только при увеличении этих ресурсов. Поэтому двойственные оценки определяют дефицитность используемых ресурсов: в оптимальном плане дефицитные ресурсы получают ненулевые оценки, а недефицитные - нулевые.

2. Несимметричная пара взаимно двойственных задач.

Рассматривается каноническая задача линейного программирования (КЗЛП):

Двойственная задача имеет вид:

3. Общая постановка взаимодвойственных задач.

Рассматривается общая задача линейного программирования (ОЗЛП):

Двойственная задача:

Замечание: Неотрицательная переменная одной задачи соответствует ограничению-неравенству другой задачи, и наоборот, ограничение-неравенство одной задачи соответствует неотрицательной переменной другой задачи.

Двойственная задача по отношению к исходной составляется согласно следующим правилам:

1. Одна задача является задачей максимизации с ограничениями , другая является задачей минимизации с ограничениями .

2. Каждому ограничению одной задачи соответствует переменная другой задачи. Номер переменной совпадает с номером ограничения.

3. Ограничению, записанному в виде неравенства, соответствует переменная двойственной задачи с условием неотрицательности.

4. Матрица условий одной задачи получается транспонированием матрицы условий другой задачи:

для исходной задачи ,

для двойственной задачи .

5. Коэффициенты целевой функции одной задачи соответствуют свободным членам системы ограничений другой задачи.

Исходя из определения, можно предложить следующий алго­ритм составления двойственной задачи:

1. Привести все неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задаче ищут мак­симум линейной функции, то все неравенства системы ог­раничений привести к виду " ", а если минимум — к виду " ",. Для этого неравенства, в которых данное требование не выполняется, умножить на (-1).

2. Составить расширенную матрицу системы исходной задачи А, в которую включить матрицу коэффициентов при переменных, столбец свободных членов системы ограничений и строку коэффициентов при переменных в линейной функции.

3. Найти матрицу , транспонированную к матрице А.

4. Сформулировать двойственную задачу на основании полученной матрицы и условия неотрицательности переменных.

Пример.1.Дана исходная задача линейного программирования:

Составить задачу, двойственную исходной задаче.

1. Так как исходная задача является задачей на максимизацию, то приведем все неравенства системы ограничений к виду " ", для этого обе части первого неравенства умножим на (-1).

Получим .

2. Составим расширенную матрицу системы А: .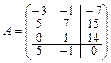

3. Найдем матрицу , транспонированную к А: .

4. Сформулируем двойственную задачу:

Пример.2.Дана исходная задача линейного программирования:

Тогда двойственная задача будет иметь вид:

.

Основное неравенство теории двойственности.

Имеется пара взаимно двойственных задач. Для любых допустимых решени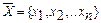й и исходной и двойственной задач справедливо неравенство или .

Достаточный признак оптимальности.

Если , - допустимые решения взаимно двойственных задач, для которых выполняется равенство , то и являются оптимальными решениями соответствующих задач.

Первая теорема двойственности.

Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая задача, причем оптимальные значения их функций равны: .

Если целевая функция одной задачи не ограничена, то условия другой задачи несовместны.

Вторая теорема двойственности.

Предположим, дана симметричная пара взаимно двойственных задач.

Отсюда можно установить соответствие между первоначальными переменными одной из взаимно- двойственных задач и дополнительными переменными другой задачи:

Для оптимальных значений переменных справедливы соотношения:

В силу условия неотрицательности переменных каждое из слагаемых должно равняться нулю:

Отсюда вытекает вторая теорема двойственности.

Положительным компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты решения другой задачи. То есть, если ,то , а если , то .

Третья теорема двойственности.

Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих свободных переменных целевой функции оптимального решения исходной задачи.

Компоненты оптимального решения двойственной задачи равны значениям частных производных целевой функции по соответствующим аргументам т.е. и характеризуют на сколько вырастут доходы если соответствующий ресурс увеличить на одну единицу.

Пример. Понятие двойственности рассмотрим на примере задачи оптимального использования ресурсов.

Для производства двух видов продукции используется три вида сырья. Предприятие имеет сырья соответственно в количествах 50, 30, 60 единиц. От реализации единицы каждого вида продукции предприятие полу­чит прибыль соответственно 17 руб. (), 25 руб. (). Нормы расхода сырья на производство товаров вместе с данными о при­были и запасах сырья представлены в следующей таблице:

Вид сырья	Нормы расхода сырья для производства единицы товара	Запасы
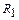
Прибыль

Пусть - объем производства товаров , обеспечивающий максимум прибыли.

Математическая модель исходной (прямой) задачи:

Поставив в соответствие каждому ограничению-неравенству одной задачи неотрицательную переменную другой задачи, запишем математическую модель двойственной задачи:

Решение взаимно двойственных задач представлено на следующих листа Mathcad:

Прямая задача (задача нахождения оптимального плана производства):

Таким образом, в результате решения прямой задачи получили оптимальный план производства: Х, при котором следует производить оба вида продукции, и прибыль от реализации будет максимальной 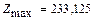рублей.

Двойственная задача (задача нахождения оптимального набора оценок на ресурсы):

Решая двойственную задачу, нашли оптимальный набор оценок на ресурсы , т.е. ресурсы 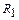и по оптимальному плану полностью использованы, и объективно обусловленные оценки этих ресурсов ненулевые (данные ресурсы являются дефицитными). Ресурс не полностью используется, и объективно условленная оценка этого ресурса нулевая (ресурс недефицитный).

7. Двойственный симплекс-метод

Двойственный симплекс-метод является методом, при котором сначала симплексным методом решается исходная задача, а затем оптимальное решение двойственной задачи находится с помощью теорем двойственности.

Пример. Составить и решить задачу, двойственную следующей задаче:

Решение.

Сформулируем задачу, двойственную для исходной задачи.

Поскольку исходная задача является задачей на отыскание максимума целевой функции, то для составления двойственной задачи, первоначально необходимо все ограничения-неравенства исходной задачи привести к виду, когда они имеют знак «≤». Для этого обе части неравенств со знаком «≥» умножим на (-1).

Тогда двойственная задача (задача минимизации целевой функции при ограничениях-неравенствах со знаком «≥») будет иметь вид:

Используя теоремы двойственности, можно не решая двойственную задачу симплексным методом, на основе последней симплекс-таблицы оптимального решения исходной задачи получить последнюю симплекс-таблицу оптимального решения двойственной задачи.

В результате решения исходной задачи линейного программирования симплексным методом следующую симплекс-таблицу соответствующую оптимальному решению (см. Таб.3.).

Согласно первой теореме двойственности, если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая задача, причем оптимальные значения их функций равны: .

Установим соответствие между переменными исходной и двойственной задач (базисным переменным одной задачи соответствуют свободные переменные другой, и наоборот):

Положительным компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи.

Подставив найденные значения в целевую функцию F, получим , что и подтверждается первой теоремой двойственности.

Составим последнюю симплекс-таблицу оптимального решения двойственной задачи по следующим правилам:

ü Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции задачи, выраженной через свободные переменные её оптимального решения;

ü Матрица коэффициентов свободных переменных симплекс-таблицы оптимального решения двойственной задачи (кроме строки целевой функции) получается путем транспонирования матрицы коэффициентов свободных переменных симплекс-таблицы оптимального решения исходной задачи с противоположными знаками;

ü Коэффициенты при свободных переменных в строке целевой функции в симплекс-таблице оптимального решения двойственной задачи равны соответствующим свободным членам симплекс-таблицы оптимального решения исходной задачи (с противоположным знаком, если исходная задача является задачей максимизации).

В результате последняя симплекс-таблица оптимального решения двойственной задачи будет иметь вид:

Базисные переменные	Свободные члены	Свободные переменные
y4	y1	y5
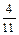
y2			-1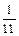
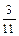
y3			-1
F			-23

при .

8. Задача целочисленного линейного программирования

Задача линейного программирования, переменные которой принимают лишь целочисленные значения, называется задачей целочисленного линейного программирования.

Математическая модель:

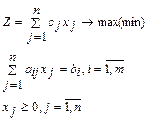
- целые.

Для решения задач целочисленного линейного программирования используется ряд методов.

Методы отсечения.

Сущность методов отсечения состоит в том, что сначала задача решается без учета целочисленности. Если полученный оптимальный план целочисленный, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:

- Ограничение должно быть линейным;

- Ограничение должно исключать из ОДР найденный оптимальный нецелочисленный план;

- Ограничение не должно исключать из ОДР ни одно целочисленное решение.

Дополнительное ограничение, обладающее указанными свойствами, называется правильным отсечением. Далее задача решается с учетом нового ограничения.

Метод Гомори (отсечения).

Этапы:

1. Решить симплекс-методом задачу линейного программирования без учета целочисленности. Если оптимальное решение целое, то это решение исходной задачи. Если целевая функция не ограничена, или ограничения несовместны, то решение целочисленной задачи линейного программирования не существует.

2. Если среди компонент есть нецелые, то необходимо выбрать компоненту с дробной частью и сформировать правильное отсечение- неравенство.

Предположим, что 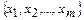- базисные переменные, - свободные переменные.

Оптимальное решение (из последней симплекс-таблицы) имеет вид . В результате оптимальное решение запишется в виде - нецелочисленное решение ( - нецелые).

Составляется неравенство правильного отсечения:

, где - дробная часть числа[1].

Правильное отсечение–неравенство преобразовать в уравнение путем введения неотрицательной целочисленной переменной и ввести это уравнение в систему ограничений.

Соотношение (1) добавляется в последнюю симплекс-таблицу как дополнительная строка. В результате симплекс-таблица представляет недопустимое решение.

4.Полученная расширенная задача снова решается симплекс–методом. Если вновь полученное оптимальное решение нецелочисленное, то итерации повторяются.

Признак несуществования оптимального целочисленного решения: Если в процессе решения появляется уравнение (выражающее базисную переменную через свободные) с нецелым свободным членом и целыми коэффициентами при свободных переменных, то исходная задача не имеет целочисленного оптимального решения.