Вычисление средней арифметической интервального ряда

Иногда среднюю арифметическую величину исчисляют по данным интервального вариационного ряда (когда варианты признака, по которому определяется средняя, представлены в виде интервалов «от – до»). В этом случае в качестве значений признаков в группах принимают середины интервалов, в результате чего образуется дискретный ряд.

Пример. Определить средний размер капитальных затрат на одно предприятие по следующим данным:

Исходные данные	Расчетные значения
Группы предприятий по размеру капитальных затрат, тыс.руб.	Число предприятий, f	Середина интервала, тыс.руб., х	x*f
До 3000
3000 – 3200
3200 – 3400
3400 – 3600
3600 – 3800
3800 и более
Итого		-

Решение. Для исчисления средней в интервальном ряду необходимо прежде всего перейти от интервального ряда к дискретному путем замены интервальных значений их средними значениями (простая средняя между верхней и нижней границами каждого интервала) (см. расчет в табл., гр. 3).

Если имеются интервалы с так называемыми открытыми границами (в нашем примере первый интервал – до 3000 тыс. руб. или последний интервал – 3800 тыс. руб.), то для расчета средней условно определяют неизвестную границу интервала. Обычно в этих условиях берут значение последующего интервала (для первого) или предыдущего (для последнего).

После того как найдено среднее значение интервалов, расчет производится по средней арифметической взвешенной.

В нашем примере средний размер капитальных затрат на одно предприятие составит:

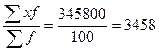= тыс.руб.

Необходимо помнить, что средняя арифметическая интервального ряда менее точна, чем средняя арифметическая, исчисленная из конкретных вариантов, потому что при исчислении середин интервалов допускается некоторая условность.

Средняя арифметическая обладает рядом свойств:

1. Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических величин:

Если х_i = y_i + z_i, то

Это правило показывает, в каких случаях можно суммировать средние величины. Если, например, выпускаемые изделия состоят из двух деталей у и z и на изготовление каждой из них расходуется в среднем у = 3 ч, z = 5 ч, то средние затраты времени на изготовление одного изделия (х) будут равны: 3 + 5 = 8 ч. то есть х = у + z.

2. Алгебраическая сумма отклонений индивидуальных значений варьирующего признака от средней равна нулю, так как сумма отклонений в одну сторону погашается суммой отклонений в другую сторону, то есть

, потому что

Это правило показывает, что средняя является равнодействующей.

3. Если все варианты ряда уменьшить или увеличить на одно и то же число а, то средняя уменьшится или увеличится на это же число а:

=

4. Если все варианты ряда уменьшить или увеличить в А раз, то средняя также соответственно уменьшится или увеличится в А раз:

=

5. Если все частоты ряда разделить или умножить на одно и же число с/, то средняя не изменится:

Это свойство показывает, что средняя зависит не от размеров весов, а от соотношения между ними. В качестве весов могут выступать не только абсолютные, но и относительные величины.

Средняя гармоническая

В статистической практике бывают случай, когда при вычислении средней имеются данные об индивидуальных значениях признака (х) и его общем объеме в совокупности (W = xf), но неизвестны частоты (f). В таком случае среднее значение признака вычисляется по формуле средней гармонической.

Средняя гармоническая – представляет собой величину, обратную средней арифметической из обратных значений вариант.

=

Пример. По данным таблицы требуется определить среднюю рентабельность капитала по двум акционерным обществам в целом.

№ АО	Рентабельность акционерного капитала, % (х)	Получено прибыли, тыс.руб. (W = xf)	Акционерный капитал, тыс.руб. (W/x)
Итого	-

Решение. Основой выбора формы средней является реальное содержание определяемого показателя:

Рентабельность, % = (Прибыль / Акционерный капитал) * 100

Средняя рентабельность равна отношению полученной предприятиями прибыли к сумме их акционерного капитала. В данном примере отсутствуют прямые данные об акционерном капитале, но его сумму можно определить косвенным путем, разделив полученную прибыль (М) на рентабельность капитала (х).

Средняя рентабельность акционерного капитала будет равна

= или 38 %.

В тех случаях, когда произведения fx одинаковы или равны единице (W=1), применяется средняя гармоническая простая, вычисляемая по формуле

=

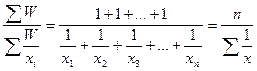
где х – отдельные варианты; n – их число

Пример. Фактический объем реализации продукции ОАО «Лада» за месяц составил 14 млн руб. При проверке было выявлено, что объем неучтенной продукции составил 15 %. Фактический объем реализации продукции ОАО «Мир» также составил 14 млн руб., а объем выявленной в результате проверки неучтенной продукции 25 %.

Определить средний процент неучтенной продукции для обоих предприятий.

Решение. Для решения этой задачи необходимо применить формулу простой средней гармонической:

=

то есть средний процент неучтенной продукции для обоих предприятий составляет 18,8 %.

Средняя геометрическая

Средняя геометрическая равна корню степени n из произведения коэффициентов роста, характеризующих отношение величины каждого последующего периода к величине предыдущего.

Средний коэффициент роста можно определить также по энным последнего и первого уровней ряда. Если первый уровень ряда обозначить у_i, а последний – у_n то

,

так как

где n – число лет, а не коэффициентов.

Приведенные формулы идентичны, но одна применяется в тех случаях, когда имеются текущие коэффициенты или темпы роста, а вторая – когда имеются абсолютные значения начального и конечного уровней ряда.

Пример. Количество зарегистрированных браков. характеризуется следующими данными:

Год
Количество зарегистрированных браков

Определить средний коэффициент роста количества браков, зарегистрированных за три года.

Решение. Определим средний коэффициент роста количества браков, зарегистрированных за три года, используя формулу средней геометрической:

а) средний коэффициент динамики зарегистрированных браков, рассчитанный по абсолютным показателям ряда динамики:

, или 109,4 %

б) средний коэффициент роста количества зарегистрированных браков, рассчитанный по цепным коэффициентам роста:

, или 109,4 %,

То есть в среднем каждый год количество зарегистрированных браков прирастало на 9,4 %.

Средняя квадратическая и средняя кубическая

В экономической практике часто возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда применяется средняя квадратическая (для вычисления средней величины стороны n квадратных участков, средних диаметров труб, стволов и т.п.) и средняя кубическая (определение средней длины стороны n кубов).

Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:

Средняя квадратическая взвешенная рассчитывается как

f – веса.

Средняя кубическая простая:

Средняя кубическая взвешенная:

Средние квадратическая и кубическая имеют ограниченное применение в статистической практике. Широко пользуется статистика средней квадратической, но не из самих вариантов х, а из их отклонений от средней () при расчете показателей вариации.

Структурные средние

Для характеристики структуры совокупности применяются особые показатели, которые называют структурными средними. К таким показателям относятся мода и медиана. В отличие от средней арифметической и средней гармонической мода и медиана совпадают с конкретным числом, имеющимся в вариационном ряду, и не всегда совпадают со средней арифметической и средней гармонической.

Модой (Mo) называется чаще всего встречающийся вариант, или то значение признака, которое соответствует максимальной точке теоретической кривой распределений.

В дискретном вариационном ряду мода – это варианта с наибольшей частотой.

Пример. При обследовании 500 семей рабочих одной из отраслей промышленности установлены следующие их размеры по количеству членов семей: