 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Упрощение логических выражений с помощью диаграмм Карно-Вейча
|
|
Карта Карно или диаграмма Вейча это определённая форма таблицы истинности. На рис 7.8. представлены карты двух, трёх и четырёх переменных. Расположение групп переменных x i не имеет значения, необходимо лишь, чтобы каждая ячейка отличалась от любой соседней лишь на одну переменную. Согласно принятой форме построения карт соседними ячейками также считаются ячейки первой и последней строк, ячейки первого и последнего столбцов. Число ячеек карты равно числу возможных комбинаций значений логических переменных и в каждую ячейку записывается значение логической функции, соответствующее данному набору переменных.

Рис.7.8.
Алгоритм минимизации логического выражения заключается в следующем.
1) На карте выделяют прямоугольные области со смежными ячейками равными 1. Каждая область должна содержать 2 k ячеек, где k – целое число. Одну и туже ячейку можно использовать более одного раза. Угловые ячейки также можно объединять в область. Можно объединять не ячейки с 1, а ячейки с нулями и взять инверсную функцию.
2) Из полученного множества выбирают минимальное число максимально больших областей и суммируют их логические функции.
Для представления функции пяти аргументов необходимо использовать две карты для четырёх переменных: одна для х 5=1 и вторая – х 5=0. Эти карты располагаются одна под другой и области охвата клеток могут быть трёхмерными, т.е. в одну область могут входить клетки двух карт.
Для функции шести аргументов используют четыре пары карт четырёх переменных с заданными 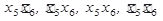 .
.
Для большего числа переменных карты не используются, а применяют алгебраические методы (метод Квайна и Мак-Класки, метод неопределённых коэффициентов и др.).
Примеры.
1) Карта для двух переменных.
Пусть  . Карта имеет вид
. Карта имеет вид

Логическая функция соответствующая выделенной области 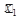 , и
, и  .
.
2) Карта трёх переменных.
Пусть карта построенная по таблице истинности имеет вид. Выделяем две области.

Полученное выражение равно  .
.
3) Карта четырёх переменных.

Внутренняя квадратная область соответствует выражению 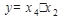 . Четыре угловых ячейки можно объединить, свернув таблицу в виде тора, и соответствующее области выражение есть
. Четыре угловых ячейки можно объединить, свернув таблицу в виде тора, и соответствующее области выражение есть  . Общее выражение тогда получиться
. Общее выражение тогда получиться 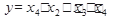 .
.
Дата публикования: 2014-10-25; Прочитано: 2918 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
