Реализация сложных логических функций на интегральных микросхемах

Учитывая ограниченный ассортимент интегральных микросхем по числу выполняемых операций для практической реализации произвольных логических функций часто необходимо представить их через единственную операцию «И-НЕ» или»ИЛИ-НЕ». Такое преобразование выполняется в три этапа.

1) Составление функционального уравнения (ФАЛ).

На этом этапе выписывают комбинации переменных для которых искомая функция – «истина» т.е. равна 1. Каждая комбинация записывается в виде произведения переменных и все полученные произведения суммируют.

Пример: рассмотрим логическую схему, применяемую для выделения сигнала из помех, а также для определения переноса в следующий разряд при поразрядном сложении чисел в двоичной системе. На вход поступают три логических сигнала. На выходе напряжение равно единице только в том случае, когда, по крайней мере, два сигнала равны 1. Данное условие можно записать

.

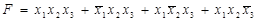Для отыскания всех возможных комбинаций переменных, обеспечивающих единичное значение функции, используют таблицы состояний.

2) Преобразование функционального уравнения с целью упрощения.

а) Использование алгебры логики.

.

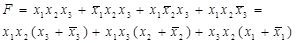Тогда

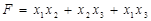(7.1).

б) Построение диаграмм Вейча или карт Карно.

3) Дальнейшее преобразование уравнения с целью приведения его к виду, реализуемому заданными интегральными схемами.

Пусть имеем только элементы «И-НЕ». Тогда уравнение (7.1) сводиться к виду согласно теореме де-Моргана

.

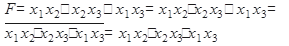Последнее выражение можно представить схемой на рис.7.7.

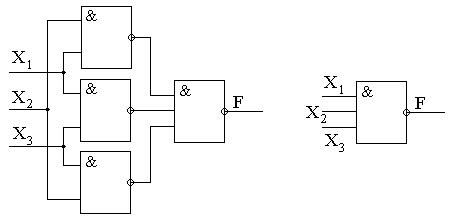
Рис.7.7.