Операционные усилители

Операционный усилитель (ОУ) – это унифицированный многокаскадный усилитель постоянного тока, как правило, выполненный в виде интегральной схемы. Он успешно применяется, как при решении многих технических задач (усиление и преобразование сигналов, стабилизация напряжения и тока и т.п.), так и при выполнении математических операций с сигналами (суммирование, вычитание, дифференцирование, интегрирование, логарифмирование и т.п.). Отсюда и название усилителя – операционный, т.е. решающий. Требование к электрическим характеристикам ОУ связаны в основном с необходимостью обеспечить: высокий коэффициент по напряжению, большое выходное и малое выходное сопротивление, линейность передаточной характеристики, высокую верхнюю частоту пропускания.

Требование у инструктивному исполнению ОУ в основном следующие: наличие двух автономных входов 1 и 2; выполнение одного из входов (1) инвертирующим (в противофазе), а другого (2) неинвертирующим (совпадение по фазе) по отношению к выходному сигналу. Обычно ОУ снабжают большим числом зажимов (до 15), необходимых для подключения дополнительных элементов контроля балансировки, коррекции частотной характеристики и других функций.

Типовая функциональная схема ОУ приведена на рис. 5.19.

Рис. 5.19. Схематическое изображение операционного усилителя:

1 — инвертирующийвход, 2 — неинвертирующий вход, 3, 4 — питание постоянным напряжением, 5 — выход

В общем виде ОУ можно представить состоящим из четырех каскадов: входного дифференциального усилителя, имеющего симметричный вход и обеспечивающего высокую стабильность, малый шум и т.п.; промежуточного усилителя напряжения с большим коэффициентом усиления; каскада сдвига уровня нуля и выходного эмиттерного повторителя выполненного по двухтактной схеме и обеспечивающего малое выходное сопротивление ОУ.

Можно определить следующие радиотехнические требования к идеальному ОУ:

1. Коэффициент усиления по напряжению бесконечно велик: K ®¥.

2. Входное сопротивление велико: R _вх®¥.

3. Выходное сопротивление мало: R _вых®0.

Свойства схем идеального ОУ определяются только внешними по отношению к ОУ элементами. Рассмотрим несколько простейших таких схем.

Инвертирующий усилитель.

Простейшей является инвертирующий усилитель, схема которого приведена на рис.5.20 (А). Инвертирующий вход ОУ соединен с выходом ОУ резистором R ₂, сигнал u ₁ подается на инвертирующий вход через резистор R ₁, а неинвертирующий вход соединен с землей.

А) Инвертирующий усилитель

Б) Неинвертирующий усилитель

Рис. 5.20 Усилители на основе ОУ.

Если принять коэффициент усиления ОУ по напряжению К =¥, а выходное напряжение ограничено, то U ₁=0, а токи определяются из выражений:

(5.20).

По первому закону Кирхгофа входной ток ОУ I _o= U ₁/ R _вх= I ₁+ I ₂.

Так как U ₁®0, a R _вх®¥, I _o также равен нулю и I ₁ = - I ₂. Выражая токи с помощью (5.20), получаем коэффициент усиления схемы:

(5.21).

Знак «минус» означает, что входной и выходной сигналы находятся в противофазе. Отметим, чтобы реальный ОУ работал как идеальный, необходимо выполнение соотношений:

(5.22),

где R _H — сопротивление цепи нагрузки. Погрешность коэффициента усиления схемы в результате невыполнения этих условий определяется по следующим формулам:

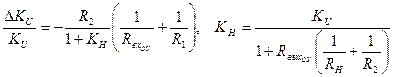(5.23).

Входное сопротивление схемы для источника сигналов определяется сопротивлением R ₁, т. е. R _вх= R ₁.

Неинвертирующий усилитель.

Здесь (рис. 5.20 (Б)) входной сигнал подается на вход (+), а по инвертирующему входу осуществляется обратная связь. Коэффициент передачи цепи обратной связи

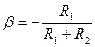_. (5.24).

Знак «минус» поставлен потому, что обратная связь подается на инвертирующий вход. Коэффициент передачи всей цепи (коэффициент усиления) равен:

_. (5.25).

Входное сопротивление схемы из-за наличия отрицательной обратной связи возрастает: , a выходное сопротивление уменьшается .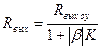

Повторитель напряжения.

В некоторых случаях не столь важным является усиление по напряжению, как способность усилителя согласовывать высокое внутреннее сопротивление источника сигналов c низким и, возможно, изменяющимся, сопротивлением нагрузки. Для этих целей используют повторитель (рис. 5.21) напряжения c полной обратной связью по инвертирующему входу: R ₁=¥, R ₂=0.

Рис. 5.21. Схема повторителя напряжения

В этом случае ; .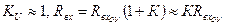

Как видно, коэффициент передачи такой цепи равен единице, входное сопротивление сильно возрастает, а выходное уменьшается. Таким образом, можно ставить низкоомную нагрузку R _н= R _вых при высокоомном сопротивлении генератора R _г= R _вх.

Сумматор.

Подадим на вход инвертирующего усилителя (рис. 5.20 (А)) сигналы как показано на рис. рис. 5.22.

Рис. 5.22. Схема сумматора.

Ток через сопротивление обратной связи R _св определяется суммой тока от каждого входного сигнала:

(5.26).

Напряжение на выходе будет равно сумме входных напряжений с весовыми функциями:

(5.27).

При одинаковых сопротивления R ₁= R ₂= R ₃ получаем простой сумматор, при сопротивлениях кратных двум или десяти, можно произвести сложение с множителями, соответствующими разрядам двоичной или десятичной системы.

Интегратор.

Данная схема (рис. 5.23) получается из схемы инвертирующего усилителя (рис. 5.20 (А)) заменой сопротивления R ₂ на емкость C, имеющую для синусоидального сигнала комплексное сопротивление . Производя замену в (5.21) для коэффициента передачи цепи, получим:

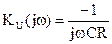(5.28).

Выражение (5.28) является условием интегрирования сигнала, так как все составляющие спектра сигнала на входе делятся на jw. Для сигнала произвольной формы получим:

(5.29).

Рис. 5.23. Схема интегратора.

В отличие от пассивной интегрирующей цепи, произведение RС здесь может быть даже меньше длительности (или периода) сигнала Т.

Дифференциатор.

Рис. 5.24. Схема дифференциатора.

Данная схема (рис. 5.24) получается из схемы интегратора, заменой местами емкости и сопротивления. Заменяя в формуле (5.21) R ₁ на 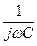и R ₂ на R, для коэффициента передачи цепи получим:

(5.30).

Это является условием дифференцирования сигнала, так как каждая составляющая спектра на входе умножается на jw. Итак,

(5.31).

Выражение (5.31) применимо при выполнении условия RC << KT, где Т — длительность сигнала, что является гораздо менее жестким условием, чем условие дифференцирования пассивной RC цепью RC << Т.

Логарифмирующие схемы.

Рис. 5.25. Логарифмирующая схема.

В цепи обратной связи ставится диод или эмиттерный диод (рис. 5.25). ВАХ p - n перехода определяется равенством 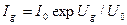, которое является достаточно точным при . Логарифмируя, получаем , отсюда

(5.32).

Суммируя выходные напряжения нескольких логарифмических усилителей, можно получить сумму логарифмов от нескольких напряжений, равную логарифму произведения этих напряжений. Обратную операцию — нахождение произведения по логарифму – можно осуществить с помощью антилогарифмической схемы, в которой диод VD и сопротивление R меняются местами.

Общим для всех рассматриваемых схем является то, что их свойства определяются не параметрами ОУ, параметрами внешних элементов (сопротивлений, емкостей и т.д.).