Методики изучения ученического коллектива

Источник: Фридман, Л.М. Изучение личности учащегося и ученических коллективов: кн. для учителя / Л.М. Фридман, Т.А. Пушкина, И.Я. Каплунович. – М.: Просвещение, 1988. – С. 163–165.

1. Методика «Идеальный класс»

Цель: выявление эталонности классного коллектива в восприятии
отдельных школьников.

Ход выполнения. Учитель должен подобрать примерно 30 положительных качеств, характеризующих классный коллектив (дружный, сплоченный, целеустремленный и т. д.), и предложить учащимся проранжировать эти качества для эталонного (идеального с их точки зрения) класса. Другими словами, каждое качество должно получить свой номер.

Ученик может рассуждать примерно так: «По моему мнению, идеальный класс должен быть, прежде всего, сплоченным. Поэтому сплоченность я ставлю на первое место и приписываю ей первый ранг. На втором месте в идеальном классе, на мой взгляд, должна стоять целеустремленность. Ей приписываю ранг 2. Дружный будет на третьем месте, поэтому ему ранг 3», и т. д. Затем ту же процедуру учащиеся должны проделать для своего класса, т. е. проранжировать все 30 качеств для класса, в котором они учатся («В нашем классе на первом месте стоит, пожалуй, дружба – ранг 1, на втором целеустремленность – ранг 2 и т. д.»).

Для удобства обработки данных эти качества удобно расположить в следующую таблицу.

Таблица

№ п/п	Качества	Ранг для идеального класса	Ранг для своего класса	Разность рангов (d)	d2
	Дружный
	Сплоченный			–8
	Целеустремленный
	И т. д.

Обработка полученных данных. На описании проранжированных
качеств для идеального (эталонного) и реального классов (см. табл.) вычисляется коэффициент корреляции r по формуле:

,

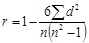где n – количество предложенных качеств (в нашем случае n = 30). Для вычисления ∑ d ² достаточно просуммировать последний столбик таблицы.

Смысл получаемого коэффициента корреляции r можно определить согласно следующей закономерности: 0 ≤ r ≤ 0,3 – слабая связь; 0,3 < r ≤ 0,5 – умеренная связь; 0,5 < r ≤ 0,7 – значительная связь; 0,7 < r ≤ 0,9 – сильная связь; 0,9 < r ≤ 1 – очень сильная связь; –1 ≤ r < 0 – противоположная
(обратная) связь.

Таким образом, чем ближе коэффициент корреляции r к единице, тем теснее связь, корреляция между эталонными и реальными классами, тем ближе ученик оценивает свой класс относительно идеального (эталонного).

2. Методика «Что важнее?»

Цель: определение ценностно-ориентационного единства класса (ЦОЕ).

Ход выполнения. Учащимся предлагается анкета, каждые пять качеств которой характеризуют отношения к учебе (1, 6, 16, 18, 25), стиль поведения и деятельности (3, 7, 9, 12, 27), знания (2, 5, 14, 21, 32), качества ума (4, 20, 30, 24, 34), учебно-организационные умения (8,13, 15, 22, 26), отношение к товарищам (11, 17, 23, 29, 33), отношение к себе (10, 19, 28, 31, 35). Школьники должны выбрать из этих 35 качеств только 5, которые, по их мнению, являются необходимыми и наиболее важными для успешного
выполнения совместной учебной работы.

Качества личности

1. Дисциплинированность.

2. Эрудированность.

3. Сознание общественного долга.

4. Сообразительность.

5. Начитанность.

6. Трудолюбие.

7. Идейная убежденность.

8. Умение контролировать работу.

9. Моральная воспитанность.

10. Самокритичность.

11. Отзывчивость.

12. Общественная активность.

13. Умение планировать работу.

14. Любознательность.

15. Умение работать с книгой.

16. Целеустремленность.

17. Коллективизм.

18. Прилежание.

19. Требовательность к себе.

20. Критичность.

21. Духовное богатство.

22. Умение объяснить задачу.

23. Честность.

24. Инициативность.

25. Внимательность.

26. Ответственность.

27. Принципиальность.

28. Самостоятельность.

29. Общительность.

30. Рассудительность.

31. Скромность.

32. Осведомленность.

33. Справедливость.

34. Оригинальность.

35. Уверенность в себе.

Обработка полученных данных. У читель составляет матрицу следующего вида.

№

Фамилия

Качества личности

…

Антонова

+

+

+

+

+

Буланова

+

+

+

+

+

Васильев

+

+

+

+

+

Дятлова

+

+

+

+

+

Иглов

+

+

+

+

+

Климов

+

+

+

+

+

Леонов

+

+

+

+

+

Никитина

+

+

+

+

+

Орехов

+

+

+

+

+

Орфеева

+

+

Павлов

+

+

+

Родных

+

+

+

+

+

Семенчук

+

+

+

+

Тимофеева

+

+

+

+

Устюгова

+

+

+

+

+

Сумма выборов

В ней в каждой строке отмечаются те пять номеров (качеств), которые выбрал данный ученик. Затем по столбцам подсчитывается количество выборов каждого качества. Коэффициент, характеризующий степень ценностно-ориентационного единства учащихся класса (С), вычисляют по следующей формуле:

,

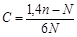где п – сумма выборов, приходящаяся на пять качеств личности, получивших максимальное число выборов, N – число учащихся, принявших участие в эксперименте. Для данных, приведенных в матрице, коэффициент ценностно-ориентированного единства класса будет равен:

.

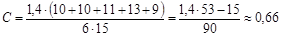С ≥ 0,5 считается высоким показателем и свидетельствует о том, что класс можно считать коллективом. Если 0,3 ≤ С < 0,5, то класс промежуточный по уровню раз­вития ЦОЕ. Наконец, С ≤ 0,3 свидетельствует о недостаточном ЦОЕ и развитии класса как коллектива. В приведенном примере
С = 0,66, что свидетельствует о высоком ценностно-ориентационном единстве школьников класса.

Если наиболее весомые качества принадлежат одной группе свойств, значит, учащиеся связывают успех своей совместной деятельности с той сферой, которую эти качества характеризуют. Например, для приведенного при­мера наиболее ценными качествами оказались сознание общественного долга (3), идейная убежденность (7), моральная воспитанность (9), которые характеризуют стиль поведения и деятельности, а также дисциплинированность (1), трудолюбие (6), характеризующие отношение к учебе. Следовательно, школьники этого класса связывают успех своей совместной деятельности прежде всего с собственным стилем поведения и деятельности, а также с положительным отношением к учебе.

3. Методика «Социометрия»

Цель: выявление межличностных отношений в классе.

Ход выполнения. Эксперимент может протекать в двух формах: путем выбора товарища по парте и «выбо­ра в действии». В первом случае учащимся предлагается подписать свой листок и написать на нем фамилии выбранных им одноклассников. Количество выборов может быть определенным (3–5 учащихся) и неопределенным (предлагается указать несколько фамилий школьников своего класса). В любом случае желательно соблюдать последовательность предпочтений (в первую (1), во вторую (2) и в третью (3) очередь). В зависимости от характера выявляемых отношений вопросы могут быть различными: «С кем бы ты хотел сидеть за одной партой?», «С кем бы ты хотел жить в одной походной палатке?», «Назови трех учеников вашего класса, которых ты рекомендовал бы для участия в дискуссии с членами молодежных организаций других стран», «С кем из учеников вашего класса ты хотел бы готовиться к контрольной работе по математике?». Одни вопросы (критерии выбора) направлены на выявление эмо­циональных связей, другие – деловых). При ответе на вопросы возможны и отрицательные выборы. Они отмечаются в таблице знаком «–».

Обработка полученных данных. На основании результатов составляется матрица, куда записывается список класса, а в верхнюю строку – номера, под которыми значатся фамилии школьников. В каждой строке против номеров учащихся, выбранных данным школьником, ставятся номера выборов (1, 2 или 3). Например, поскольку Леонов выбрал 1) Васильева, 2) Углова, 3) Климова, то ставятся соответствующие выборы на пересечении седьмой строки со столбцами 3, 5 и 6.

Если ученики выбрали друг друга (например, по данным приведенной матрицы Антонова выбрала: № 4 Дятлову, а Дятлова выбрала № 1 – Антонову), то эти два выбора (с координатами (1,4) и (4,1) обводятся в кружочек (взаимный выбор). В таблице они показаны курсивом. Номера мальчиков обычно обводятся треугольниками, девочек – кружочками. Затем на отдельном листе вычерчивается социограмма.