Метод инструментальных переменных

Для получения несмещенных (по крайней мере состоятельных) оценок параметров эконометрических моделей в ситуациях, когда имеют место (теоретически допускаются) корреляционные взаимосвязи между независимыми переменными x_it и ошибкой e_t, теория рекомендует подходы и методы, основанные на использовании инструментальных переменных.

Напомним, что в тех случаях, когда некоторые столбцы матрицы значений независимых переменных Х и вектор-столбец ошибки e взаимосвязаны между собой, математическое ожидание второго слагаемого в правой части выражения (2.9) отлично от нуля, M [(Х ¢ Х) ^{– 1} Х ¢× e ]¹0, и, следовательно, например, оценки МНК параметров модели, определяемые согласно известному выражению а =(Х ¢ Х) ^{– 1} Х ¢× у, оказываются смещенными, поскольку

M [ a – а ]= M [(Х ¢ Х) ^{– 1} Х ¢× e ]¹0. (3.51)

Заметим, что появление смещения у оценок МНК всех параметров моделей вызывает присутствие только одной независимой переменной, например, x_i,связанной с ошибкой e. В этом случае непосредственно видно, что произведение Х ¢× e =(0,..., 0, с_i, 0,...,0)¢, где константа стоит на месте, соответствующем i -й переменной, и, таким образом, имеем (Х ¢ Х) ^{– 1}¢× e = с_i ×(s _{0 i} , s _{1 i} ,..., s_ni)¢= = с_i × s _i, где s_ji – j -й элемент i -го столбца s _i матрицы (Х ¢ Х) ^{– 1}. Из полученного результата вытекает, что в соответствии с выражением (2.9) имеем а = a + с_i × s _i. Из чего следует, что смещенными оказываются все оценки коэффициентов модели.

В эконометрике обычно исследуются асимптотические свойства оценок параметров моделей. В этом случае, если в пределе при Т ®¥ существует зависимость между столбцами матрицы Х и ошибкой модели e, т. е.

то оценки МНК параметров эконометрической модели являются несостоятельными (а, следовательно, и асимптотически смещенными).

Это непосредственно вытекает из того факта, что второе слагаемое в правой части выражения

plim(a)=

отлично от нуля, поскольку из начальных условий (предположений) (2.42) вытекает, что

Использование инструментальных переменных теоретически позволяет устранить отрицательные последствия взаимосвязей независимых переменных и ошибки модели e, связанные с несостоятельностью оценок МНК параметров линейных эконометрических моделей.

Формально, без излишней строгости, выражение для вектора оценок МНК параметров эконометрической модели с использованием инструментальных переменных может быть получено следующим образом.

Предположим, что существуют так называемые “инструментальные” переменные z_i, число которых в общем случае совпадает с числом независимых факторов модели х_i, i =1,2,..., n; и при t =1,2,..., Т, каждая из которых характеризуется нулевыми корреляционными взаимосвязями с ошибкой эконометрической модели e. При заданном Т матрица значений инструментальных переменных Z имеет такой же размер, как матрица Х.

Умножим слева векторно-матричное уравнение на матрицу у = Х × a + e на матрицу Z ¢. Получим

Z ¢ у = Z ¢ Х × a + Z ¢× e, (3.53)

С учетом того, что M [ Z ¢× e ]=0, умножая выражение (3.53) слева на (Z ¢ Х) ^{– 1}, непосредственно имеем

a _z =(Z ¢ Х) ^{– 1} Z ¢ у, (3.54)

где a _z – вектор оценок параметров эконометрической модели, полученный с использованием инструментальных переменных.

Результат (3.54) можно получить и традиционным путем. Для этого обозначим у _*= Z ¢ у; Х _*= Z ¢ Х; e _*= Z ¢× e. В этом случае выражение (3.53) имеет традиционный для эконометрической модели вид:

у _*= Х _*× a + e _*. (3.55)

Используя для модели (3.55) традиционный для МНК критерий минимума суммы квадратов ошибки

s _*²=(e _*¢, e _*)=(e ¢ Z × Z ¢× e)=(Z ¢ у – Z ¢ Х × a)¢(Z ¢ у – Z ¢ Х × a)®min (3.56)

и приравнивая вектор производных показателя s _*² по вектору параметров a к нулю, , непосредственно получим следующее выражение для вектора оценок этих параметров:

a _z =(Х ¢ Z Z ¢ Х) ^{– 1} Х ¢ ZZ ¢× у. (3.57)

Далее, принимая во внимание, что произведения матриц Х ¢ Z и Z ¢ Х равны между собой, т. е. Х ¢ Z = Z ¢ Х, выражение (3.57) несложно привести к виду (3.54).

a _z =(Х ¢ ZZ ¢ Х) ^{– 1} Х ¢ ZZ ¢× у =(Х ¢ Z) ^{– 1}(Х ¢ Z) ^{– 1} Х ¢ ZZ ¢× у =(Х ¢ Z) ^{– 1} Z ¢× у =

=(Z ¢ Х) ^{– 1} Z ¢× у.

Покажем также, что при наличии у матрица Z размерностью Т ´(п +1) в пределе при Т ®¥ следующих свойств:

plim Z ¢× e)=0; (3.58)

plim Z ¢× Х)= å _{Z ¢ Х}; (3.59)

plim Z ¢× Z)= å _{Z ¢ Z}, (3.60)

где матрицы å _ZХ и å _ZZ существуют и не вырождены, оценки параметров эконометрической модели, определенные выражением (3.54), являются состоятельными.

Для этого, как и при выводе выражения (2.9), подставим вместо вектора у в формулу (3.54) у = Х × a + e. Получим

a _z = a +(Z ¢ Х) ^{– 1} Z ¢ e, (3.61)

В пределе при Т ®¥ имеем

plim a _z = a +plim Z ¢ Х) ^{– 1}× plim Z ¢ e)= a + å ^{– 1} _{Z ¢ Z} ×0= a. (3.62)

Обратим внимание на некоторые свойства оценок параметров, полученных с использованием инструментальных переменных на основе выражения (3.54).

В частности, отметим, что в общем случае эти оценки являются неэффективными. В самом деле, вид ковариационной матрицы ошибки e _*= Z ¢× e модели (3.53) свидетельствует о наличии в ее ряду автокорреляционных зависимостей даже в том случае, когда эти зависимости отсутствовали у ошибки e:

Cov (e _*)= M [ e _*¢, e _*]= M [ Z ¢× e × e ¢ Z)= s_e (Z ¢ Z). (3.63)

В этом случае ковариационная матрица оценок a _z параметров модели (3.53) имеет следующий вид:

Cov (a _z)= M [(a _z – a)(a _z – a)¢]= M [(Z ¢ Х) ^{– 1} Z ¢ e × e ¢ Z (Z ¢ Х) ^{– 1}]=

= s_e ²(Z ¢ Х) ^{– 1} Z ¢× Z (Z ¢ Х) ^{– 1}, (3.64)

где дисперсия ошибки s_e ² на практике может быть оценена на основании следующего выражения:

В пределе при Т ®¥ с учетом предположений (3.59) и (3.60) можно определить асимптотическую ковариационную матрицу оценок a _z на основании следующего выражения:

asy.var(a _z)= 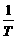plim[ T (a _z – a)(a _z – a)¢]=

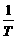= plim[ T (Z ¢ Х) ^{– 1} Z ¢ e × e ¢ Z (Х ¢ Z) ^{– 1}]=

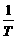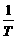= plim( Z ¢ Х) ^{– 1})plim( 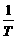Z ¢ e × e ¢ Z)plim( 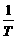Х ¢ Z) ^{– 1}=

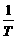= s_e ² å ^{– 1} _{Z ¢ Х} å _{Z ¢ Z} å ^{– 1} _{Z ¢ Х}. (3.66)

Для получения эффективных оценок на базе инструментальных переменных можно использовать обобщенных МНК. Для ковариационной матрицы ошибок модели, определенной выражением (3.63), оценки коэффициентов, полученные с использованием этого метода, определяются на основании следующего выражения, вытекающего из формулы (3.57):

a _{z .0}=(Х ¢ Z (Z ¢ Z) ^{– 1} Z ¢ Х) ^{– 1} Х ¢ Z (Z ¢ Z) ^{– 1}× у =(Х ¢ Р _z Х) ^{– 1} Х ¢ Р _z × у, (3.67)

где Р _z = Z (Z ¢ Z) ^{– –1}.

Несложно показать, что ковариационная матрица оценок обобщенного МНК для инструментальных переменных имеет следующий вид:

Сov (a _{z .0})= s_e ²(Х ¢ Р _z Х) ^{– 1}, (3.68)

где на практике дисперсия ошибки s_e ² определяется следующим выражением:

Вектор оценок a _{z .0}, полученный на основании формулы (3.67) является асимптотически несмещенным. Это следует из выражения:

a _{z .0}= a +( 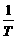Х ¢ Р _z Х) ^{– 1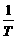}( Х ¢ Р _z ε), (3.70)

где

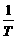(Х ¢ Р _z Х)=( 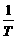Х ¢ Z)( 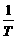Z ¢ Z) ^{– 1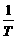}( Z ¢ X),

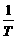(Х ¢ Р _z e)=( 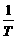Х ¢ Z)( 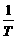Z ¢ Z) ^{– 1}( Z ¢ e).

Переходя в выражении (3.70) к пределу при Т ®¥, с учетом свойств (3.58)–(3.60) получим

plim a _{z .0}= a +(å _{Х ¢ Z} å ^{– 1} _{Z ¢ Z} å _{Z ¢ Х}) ^{– 1} å _{Z ¢ Х} å ^{– 1} _{Z ¢ Z} ×0= a. (3.71)

Однако заметим, что на практике обобщенный МНК для оценки параметров моделей с инструментальными переменными применяется не часто. Это связано с тем, что дисперсии оценок их параметров, полученных на основе выражения (.41), при удачном подборе инструментальных переменных увеличиваются не столь значительно, и такую потерю эффективности во внимание можно не принимать.

В самом деле, если инструментальные переменные z_i характеризуются достаточно сильной корреляционной связью (коэффициент парной корреляции r _{z , x} ®1) с соответствующими независимыми переменными х_i, то при одинаковых масштабах этих переменных произведения матриц Z ¢ Z и Z ¢ X будут приблизительно равными между собой и в этом случае, как это следует из выражения (3.64),

Cov (a _z)» s_e ²(Z ¢ Х) ^{– 1}» s_e ²(Х ¢ Х) ^{– 1}. (3.72)

И, наоборот, если переменные z_i и х_i слабо взаимосвязаны между собой, то диагональные элементы матрицы (Z ¢ Х) ^{– 1} в силу того, что определитель ½ Z ¢ Х ½уменьшается, существенно возрастают. В этом случае при использовании выражения (3.54) за несмещенность оценок приходится платить падением их эффективности. Этот вывод достаточно очевиден при рассмотрении однофакторной модели y_t = a ₀+ a ₁ x_t + e_t, при оценке параметров которой используется инструментальная переменная z_t.

Несложно видеть, что оценка коэффициента a ₁ в этом случае согласно выражению (3.54) определяется по следующей формуле:

а выборочная дисперсия этой оценки по формуле:

где дисперсия s_e ² определена выражением типа (3.65) при п =1.

Из выражения (3.73) непосредственно видно, что при слабой зависимости между переменными х_t и z_t его знаменатель уменьшается (в пределе до нуля), и выборочная дисперсия параметра a_z может стать как угодно большой.

Вследствие этого на практике инструментальные переменные z_i стремятся выбирать согласно следующему правилу: переменные z_i должны иметь сильные корреляционные связи с соответствующими переменными х_i и быть независимыми по отношению к ошибке модели e.

Выполнение этого правила в эконометрических исследованиях реальных процессов, для которых характерной чертой является корреляционная связь между независимыми факторами и ошибкой, достигается с помощью некоторых специальных приемов, правил формирования инструментальных переменных. Эти правила будут рассмотрены в соответствующих разделах данного учебника (см. главы V и VIII).

В заключении данного раздела рассмотрим некоторые особенности формирования матрицы инструментальных переменных Z. Очевидно, что общее число таких переменных должно быть равно количеству независимых факторов в модели. При этом, если какая-либо из переменных х_i оказывается не связанной с ошибкой e, то она сама может выступать в качестве “инструментальной” переменной. В результате матрицу Х можно представить в следующем виде:

Х =[ Х ₁ Х ₂],

где подматрица Х ₁ объясняет переменные, независимые по отношению к ошибке модели e, а подматрица Х ₂ – зависимые.

В этом случае матрица Z имеет следующий вид:

Z =[ Х ₁ Z ₂],

где Z ₂ подматрица инструментальных переменных, замещающих независимые факторы, образующие матрицу Х ₂.

Заметим также, что выражение Z (Z ¢ Z) ^{– 1} Z ¢ Х = Р _z Х = , используемое в формуле (3.67), может рассматриваться как матрица расчетных значений факторов х_it, полученных как оценки зависимых переменных при использовании в качестве независимых факторов инструментальных переменных z_i, i =1,2,..., п. В самом деле, выражение (Z ¢ Z) ^{– 1} Z ¢ х _i определяет оценки коэффициентов следующей модели:

и, таким образом, (Z ¢ Z) ^{– 1} Z ¢ Х = B, где B – матрица оценок коэффициентов моделей типа (3.74) для i =1,2,... п; имеющая следующий вид:

Тогда матрица Z ¢ B = представляет собой матрицу расчетных значений независимых факторов исходной модели, полученных в результате их выражения эконометрическими моделями типа (3.74) в зависимости от выбранных значений инструментальных переменных.

Отметим также, что если значения инструментальных переменных и независимых факторов исходной модели равны между собой, т. е. Z = X, тогда = Х (Х ¢ Х) ^{– 1} Х ¢ Х = Х.

С учетом этого равенства получим, что при частичной замене исходных факторов на инструментальные переменные матрица Z будет иметь следующий вид:

Z =[ Х ₁ ],

где = Z (Z ¢ Z) ^{– 1} Z ¢ Х ₂ и Z =[ Х ₁ Z ₂].

Вопросы к главе III

1. Как выглядит ковариационная матрица ошибок модели при наличии автокорреляционных связей в ряду ошибки e_t?

2. Как выглядит ковариационная матрица ошибок модели при наличии гетероскедастичности ошибок?

3. Каковы последствия автокорреляции и гетероскедастичности ошибок?

4. В чем суть обобщенного МНК (ОМНК)?

5. Как определяется ковариационная матрица ОМНК-оценок параметров?

6. Каковы предпосылки обобщенного метода максимального правдоподобия?

7. В чем суть двухшагового МНК Дарбина?

8. В чем суть взвешенного МНК?

9. В чем суть метода инструментальных переменных?