Векторная алгебра 1 страница

8. Домашнє завдання № 183, № 183

B 6 № 286233.

Перед на­ча­лом пер­во­го тура чем­пи­о­на­та по шаш­кам участ­ни­ков раз­би­ва­ют на иг­ро­вые пары слу­чай­ным об­ра­зом с по­мо­щью жре­бия. Всего в чем­пи­о­на­те участ­ву­ет 36 ша­ши­стов, среди ко­то­рых 15 участ­ни­ков из Рос­сии, в том числе Ев­ге­ний Ко­ро­тов. Най­ди­те ве­ро­ят­ность того, что в пер­вом туре Ев­ге­ний Ко­ро­тов будет иг­рать с каким-либо ша­ши­стом из Рос­сии?

Ре­ше­ние.

В пер­вом туре Ев­ге­ний Ко­ро­тов может сыг­рать с 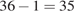ша­ши­ста­ми, из ко­то­рых 14 — из Рос­сии. Зна­чит ве­ро­ят­ность того, что в пер­вом туре Ев­ге­ний Ко­ро­тов будет иг­рать с каким-либо ша­ши­стом из Рос­сии, равна

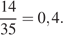
Ответ: 0,4.

Ответ: 0,4

0,4

2. B 6 № 505397. Перед на­ча­лом пер­во­го тура чем­пи­о­на­та по на­столь­но­му тен­ни­су участ­ни­ков раз­би­ва­ют на иг­ро­вые пары слу­чай­ным об­ра­зом с по­мо­щью жре­бия. Всего в чем­пи­о­на­те участ­ву­ет 16 спортс­ме­нов, среди ко­то­рых 7 участ­ни­ков из Рос­сии, в том числе Пла­тон Кар­пов. Ка­ко­ва ве­ро­ят­ность того, что в пер­вом туре Пла­тон Кар­пов будет иг­рать с каким-либо спортс­ме­ном из Рос­сии?

Ре­ше­ние.

В пер­вом туре Пла­тон Кар­пов может сыг­рать с 16 − 1 = 15 тен­ни­си­ста­ми, из ко­то­рых 7 − 1 = 6 из Рос­сии. Зна­чит, ве­ро­ят­ность того, что в пер­вом туре Пла­тон Кар­пов будет иг­рать с каким-либо тен­ни­си­стом из Рос­сии, равна

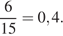
Ответ: 0,4.

Ответ: 0,4

0,4

B 6 № 315953.

В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют че­ты­ре­жды. Най­ди­те ве­ро­ят­ность того, что решка вы­па­дет ровно два раза.

Ре­ше­ние.

Рав­но­воз­мож­ны 2⁴ = 16 ис­хо­дов экс­пе­ри­мен­та: орёл-орёл-орёл-орёл, орёл-орёл-орёл-решка, орёл-орёл-решка-орёл, орёл-решка-орёл-орёл, решка-орёл-орёл-орёл, решка-решка-орёл-орёл, решка-орёл-орёл-решка, орёл-орёл-решка-решка, орёл-решка-орёл-решка, решка-орёл-решка-орёл, орёл-решка-решка-орёл, решка-решка-решка-орёл, решка-решка-орёл-решка, решка-орёл-решка-решка, орёл-решка-решка-решка, решка-решка-решка-решка

Решка вы­па­да­ет ровно два раз в шести слу­ча­ях: орёл-орёл-решка-решка, решка-орёл-орёл-решка, решка-решка-орёл-орёл, решка-орёл-решка-орёл, орёл-решка-орёл-решка, орёл-решка-решка-орёл. По­это­му ве­ро­ят­ность того, что орел вы­па­дет ровно 2 раза, равна

.

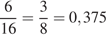Ответ: 0,375.

Ответ: 0.375

0.375

4. B 6 № 320198. Ве­ро­ят­ность того, что на тесте по био­ло­гии уча­щий­ся О. верно решит боль­ше 11 задач, равна 0,67. Ве­ро­ят­ность того, что О. верно решит боль­ше 10 задач, равна 0,74. Най­ди­те ве­ро­ят­ность того, что О. верно решит ровно 11 задач.

Ре­ше­ние.

Рас­смот­рим со­бы­тия A = «уча­щий­ся решит 11 задач» и В = «уча­щий­ся решит боль­ше 11 задач». Их сумма — со­бы­тие A + B = «уча­щий­ся решит боль­ше 10 задач». Со­бы­тия A и В не­сов­мест­ные, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий:

P(A + B) = P(A) + P(B).

Тогда, ис­поль­зуя дан­ные за­да­чи, по­лу­ча­ем: 0,74 = P(A) + 0,67, от­ку­да P(A) = 0,74 − 0,67 = 0,07.

Ответ: 0,07.

Ответ: 0,07

0,07

5. B 6 № 320169. Вася, Петя, Коля и Лёша бро­си­ли жре­бий — кому на­чи­нать игру. Най­ди­те ве­ро­ят­ность того, что на­чи­нать игру дол­жен будет Петя.

Ре­ше­ние.

Жре­бий на­чать игру может вы­пасть каж­до­му из че­ты­рех маль­чи­ков. Ве­ро­ят­ность того, что это будет имен­но Петя, равна одной чет­вер­той.

Ответ: 0,25.

Ответ: 0,25

0,25

B 6 № 283465.

В слу­чай­ном экс­пе­ри­мен­те бро­са­ют две иг­раль­ные кости. Най­ди­те ве­ро­ят­ность того, что в сумме вы­па­дет 10 очков. Ре­зуль­тат округ­ли­те до сотых.

Ре­ше­ние.

Ко­ли­че­ство ис­хо­дов, при ко­то­рых в ре­зуль­та­те брос­ка иг­раль­ных ко­стей вы­па­дет 10 очков, равно 3: 4+6, 5+5, 6+4. Каж­дый из ку­би­ков может вы­пасть ше­стью ва­ри­ан­та­ми, по­это­му общее число ис­хо­дов равно 6·6 = 36. Сле­до­ва­тель­но, ве­ро­ят­ность того, что в сумме вы­па­дет 10 очков, равна

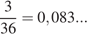
Ответ: 0,08.

Ответ: 0,08

0,08

7. B 6 № 320170. В чем­пи­о­на­те мира участ­ву­ют 16 ко­манд. С по­мо­щью жре­бия их нужно раз­де­лить на че­ты­ре груп­пы по че­ты­ре ко­ман­ды в каж­дой. В ящике впе­ре­меш­ку лежат кар­точ­ки с но­ме­ра­ми групп:

1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.

Ка­пи­та­ны ко­манд тянут по одной кар­точ­ке. Ка­ко­ва ве­ро­ят­ность того, что ко­ман­да Рос­сии ока­жет­ся во вто­рой груп­пе?

Ре­ше­ние.

Ве­ро­ят­ность того, что ко­ман­да Рос­сии ока­жет­ся во вто­рой груп­пе, равна от­но­ше­нию ко­ли­че­ства кар­то­чек с но­ме­ром 2, к об­ще­му числу кар­то­чек. Тем самым, она равна

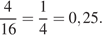
Ответ: 0,25.

Ответ: 0,25

0,25

8. B 6 № 500998. В кар­ма­не у Пети было 2 мо­не­ты по 5 руб­лей и 4 мо­не­ты по 10 руб­лей. Петя, не глядя, пе­ре­ло­жил какие-то 3 мо­не­ты в дру­гой кар­ман. Най­ди­те ве­ро­ят­ность того, что пя­ти­руб­ле­вые мо­не­ты лежат те­перь в раз­ных кар­ма­нах.

Ре­ше­ние.

Чтобы пя­ти­руб­ле­вые мо­не­ты ока­за­лись в раз­ных кар­ма­нах, Петя дол­жен взять из кар­ма­на одну пя­ти­руб­ле­вую и две де­ся­ти­руб­ле­вые мо­не­ты. Это можно сде­лать тремя спо­со­ба­ми: 5, 10, 10; 10, 5, 10 или 10, 10, 5. Эти со­бы­тия не­сов­мест­ные, ве­ро­ят­ность их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий:

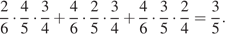
Дру­гое рас­суж­де­ние.

Ве­ро­ят­ность того, что Петя взял пя­ти­руб­ле­вую мо­не­ту, затем де­ся­ти­руб­ле­вую, и затем еще одну де­ся­ти­руб­ле­вую (в ука­зан­ном по­ряд­ке) равна

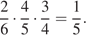
По­сколь­ку Петя мог до­стать пя­ти­руб­ле­вую мо­не­ту не толь­ко пер­вой, но и вто­рой или тре­тьей, ве­ро­ят­ность до­стать набор из одной пя­ти­руб­ле­вой и двух де­ся­ти­руб­ле­вых монет в 3 раза боль­ше. Тем самым, она равна 0,6.

Ответ: 0,6.

При­ве­дем дру­гое ре­ше­ние.

Ко­ли­че­ство спо­со­бов взять 3 мо­не­ты из 6, чтобы пе­ре­ло­жить их в дру­гой кар­ман, равно 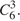Ко­ли­че­ство спо­со­бов вы­брать 1 пя­ти­руб­ле­вую мо­не­ту из 2 пя­ти­руб­ле­вых монет и взять вме­сте с ней еще 2 де­ся­ти­руб­ле­вых мо­не­ты из име­ю­щих­ся 4 де­ся­ти­руб­ле­вых монет по пра­ви­лу про­из­ве­де­ния равно 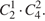По­это­му ис­ко­мая ве­ро­ят­ность того, что пя­ти­руб­ле­вые мо­не­ты лежат в раз­ных кар­ма­нах, равна

Ответ: 0,6

0,6

9. B 6 № 500997. В клас­се учит­ся 21 че­ло­век. Среди них две по­дру­ги: Аня и Нина. Класс слу­чай­ным об­ра­зом делят на 7 групп, по 3 че­ло­ве­ка в каж­дой. Найти ве­ро­ят­ность того. что Аня и Нина ока­жут­ся в одной груп­пе.

Ре­ше­ние.

Пусть Аня ока­за­лась в не­ко­то­рой груп­пе. Тогда для 20 остав­ших­ся уча­щих­ся ока­зать­ся с ней в одной груп­пе есть две воз­мож­но­сти. Ве­ро­ят­ность этого со­бы­тия равна 2: 20 = 0,1.

При­ве­дем ком­би­на­тор­ное ре­ше­ние.

Всего спо­со­бов вы­брать 3 уча­щих­ся из 21 уча­ще­го­ся клас­са равно 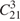. Вы­брать пару «Аня и Нина» и по­ме­стить их в одну из семи групп можно спо­со­ба­ми. До­ба­вить в эту груп­пу еще од­но­го из остав­ших­ся 19 уча­щих­ся можно спо­со­ба­ми. По­это­му ве­ро­ят­ность того, что де­воч­ки ока­жут­ся в одной груп­пе равна

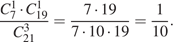
При­ве­дем еще одно ре­ше­ние.

Рас­смот­рим первую груп­пу. Ве­ро­ят­ность того, что Аня ока­жет­ся в ней, равна 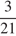. Если Аня уже на­хо­дит­ся в пер­вой груп­пе, то ве­ро­ят­ность того, что Нина ока­жет­ся этой же груп­пе равна 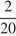. По­сколь­ку все семь групп рав­но­прав­ны, ве­ро­ят­ность того, что по­дру­ги ока­жут­ся в одной груп­пе, равна

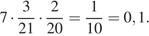
Ответ: 0,1.

Ответ: 0,1

0,1

10. B 6 № 320201. В ма­га­зи­не три про­дав­ца. Каж­дый из них занят с кли­ен­том с ве­ро­ят­но­стью 0,3. Най­ди­те ве­ро­ят­ность того, что в слу­чай­ный мо­мент вре­ме­ни все три про­дав­ца за­ня­ты од­но­вре­мен­но (счи­тай­те, что кли­ен­ты за­хо­дят не­за­ви­си­мо друг от друга).

Ре­ше­ние.

Ве­ро­ят­ность про­из­ве­де­ния не­за­ви­си­мых со­бы­тий равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий. По­это­му ве­ро­ят­ность того, что все три про­дав­ца за­ня­ты равна

Ответ: 0,027.

Ответ: 0,027

0,027

11. B 9 № 7321. На ри­сун­ке изоб­ра­жен гра­фик функ­ции 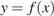, опре­де­лен­ной на ин­тер­ва­ле 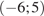. Най­ди­те ко­ли­че­ство точек, в ко­то­рых ка­са­тель­ная к гра­фи­ку функ­ции па­рал­лель­на пря­мой .

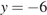Ре­ше­ние.

По­сколь­ку ка­са­тель­ная па­рал­лель­на пря­мой y = −6 или сов­па­да­ет с ней, их уг­ло­вые ко­эф­фи­ци­ен­ты равны 0. Уг­ло­вой ко­эф­фи­ци­ент ка­са­тель­ной равен зна­че­нию про­из­вод­ной в точке ка­са­ния. Про­из­вод­ная равна нулю в точ­ках экс­тре­му­ма функ­ции. На за­дан­ном ин­тер­ва­ле функ­ция имеет 3 мак­си­му­ма и 4 ми­ни­му­ма, итого 7 экс­тре­му­мов. Таким об­ра­зом, ка­са­тель­ная к гра­фи­ку функ­ции па­рал­лель­на пря­мой y = −6 или сов­па­да­ет с ней в 7 точ­ках.

Ответ: 7.

Ответ: 7

B 9 № 121715.

Пря­мая яв­ля­ет­ся ка­са­тель­ной к гра­фи­ку функ­ции . Най­ди­те c.

Ре­ше­ние.

Усло­вие ка­са­ния гра­фи­ка функ­ции и пря­мой 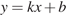задаётся си­сте­мой тре­бо­ва­ний:

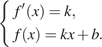
В нашем слу­чае имеем:

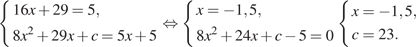
Таким об­ра­зом, с = 23.

Ответ: 23.

Ответ: 23

13. B 9 № 505145. На ри­сун­ке изоб­ра­же­ны гра­фик функ­ции y = f (x) и ка­са­тель­ная к нему в точке с абс­цис­сой x ₀. Най­ди­те зна­че­ние про­из­вод­ной функ­ции f (x) в точке x ₀.

Ре­ше­ние.

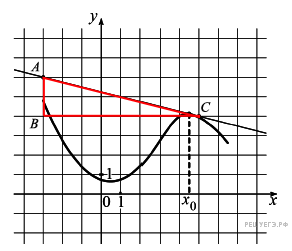Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной, ко­то­рый в свою оче­редь равен тан­ген­су угла на­кло­на дан­ной ка­са­тель­ной к оси абс­цисс. По­стро­им тре­уголь­ник с вер­ши­на­ми в точ­ках A (−3; 6), B (−3; 4), C (5; 4). Угол на­кло­на ка­са­тель­ной к оси абс­цисс будет равен углу, смеж­но­му с углом ACB:

.

Ответ: −0,25.

Ответ: -0,25

-0,25

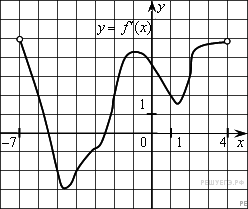
14. B 9 № 27497. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−7; 4). Най­ди­те про­ме­жут­ки воз­рас­та­ния функ­ции f(x). В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.

Ре­ше­ние.

Про­ме­жут­ки воз­рас­та­ния дан­ной функ­ции f(x) со­от­вет­ству­ют про­ме­жут­кам, на ко­то­рых ее про­из­вод­ная по­ло­жи­тель­на, то есть ин­тер­ва­лам (−7; −5,5), (−2,5; 4). Дан­ные ин­тер­ва­лы со­дер­жат целые точки –6, –2, –1, 0, 1, 2, 3. Их сумма равна –3.

Ответ: –3.

Ответ: -3

-3

B 9 № 6041.

Пря­мая 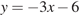па­рал­лель­на ка­са­тель­ной к гра­фи­ку функ­ции . Най­ди­те абс­цис­су точки ка­са­ния.

Ре­ше­ние.

Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной. По­сколь­ку ка­са­тель­ная па­рал­лель­на пря­мой 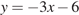их уг­ло­вые ко­эф­фи­ци­ен­ты равны. По­это­му абс­цис­са точки ка­са­ния на­хо­дит­ся из урав­не­ния :

.

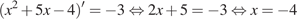Ответ: −4.

Ответ: -4

-4

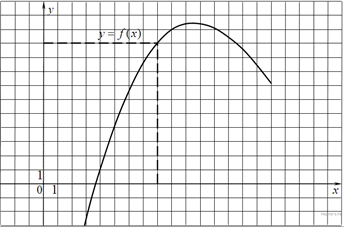
16. B 9 № 40129. На ри­сун­ке изоб­ра­жен гра­фик функ­ции y=f(x). Пря­мая, про­хо­дя­щая через на­ча­ло ко­ор­ди­нат, ка­са­ет­ся гра­фи­ка этой функ­ции в точке с абс­цис­сой 8. Най­ди­те f' (8).

Ре­ше­ние.

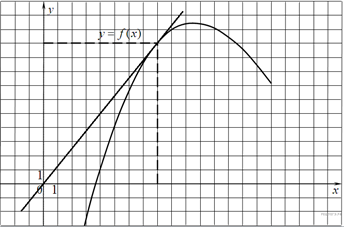По­сколь­ку ка­са­тель­ная про­хо­дит через на­ча­ло ко­ор­ди­нат, ее урав­не­ние имеет вид y = kx. Эта пря­мая про­хо­дит через точку (8; 10), по­это­му 10 = 8 · k, от­ку­да k = 1,25. По­сколь­ку уг­ло­вой ко­эф­фи­ци­ент ка­са­тель­ной равен зна­че­нию про­из­вод­ной в точке ка­са­ния, по­лу­ча­ем: f' (8) = 1,25.

Ответ: 1,25.

Ответ: 1,25

1,25

B 9 № 122215.

Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну 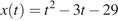(где x —рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость (в м/с) в мо­мент вре­ме­ни t = 3 с.

Ре­ше­ние.

Най­дем закон из­ме­не­ния ско­ро­сти:

.

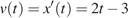Тогда на­хо­дим:

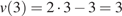м/с.

Ответ: 3.

Ответ: 3

18. B 9 № 7089.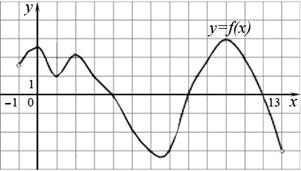

На ри­сун­ке изоб­ра­жен гра­фик функ­ции y = f (x), опре­де­лен­ной на ин­тер­ва­ле (−1; 13). Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции по­ло­жи­тель­на.

Ре­ше­ние.

Про­из­вод­ная функ­ции по­ло­жи­тель­на на тех ин­тер­ва­лах, на ко­то­рых функ­ция воз­рас­та­ет, т. е. на ин­тер­ва­лах (−1; 0), (1; 2) и (6,6; 10). В них со­дер­жат­ся целые точки 7, 8 и 9. Всего 3 точки.

Ответ: 3.

Ответ: 3

B 9 № 54801.

На ри­сун­ке изоб­ра­жен гра­фик функ­ции y=f(x). Пря­мая, про­хо­дя­щая через на­ча­ло ко­ор­ди­нат, ка­са­ет­ся гра­фи­ка этой функ­ции в точке с абс­цис­сой 10. Най­ди­те f' (10).

Ре­ше­ние.

Зна­че­ние про­из­вод­ной в точке ка­са­ния равно уг­ло­во­му ко­эф­фи­ци­ен­ту ка­са­тель­ной. По­сколь­ку ка­са­тель­ная про­хо­дит через на­ча­ло ко­ор­ди­нат, ее урав­не­ние имеет вид y=kx. Пря­мая про­хо­дит через точку (10; −6), зна­чит, k =−0,6. По­сколь­ку уг­ло­вой ко­эф­фи­ци­ент равен зна­че­нию про­из­вод­ной в точке ка­са­ния по­лу­ча­ем: f' (10)=−0,6.

Ответ: −0,6.

Ответ: -0,6

-0,6

20. B 9 № 323475. На ри­сун­ке изоб­ражён гра­фик не­ко­то­рой функ­ции . Функ­ция 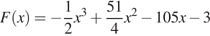— одна из пер­во­об­раз­ных функ­ции 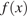. Най­ди­те пло­щадь за­кра­шен­ной фи­гу­ры.

Ре­ше­ние.

Най­дем фор­му­лу, за­да­ю­щую функ­цию 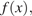гра­фик ко­то­рой изоб­ражён на ри­сун­ке.

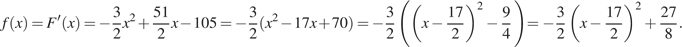
Сле­до­ва­тель­но, гра­фик функ­ции 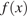по­лу­чен сдви­гом гра­фи­ка функ­ции 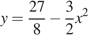на 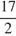еди­ниц впра­во вдоль оси абс­цисс. По­это­му ис­ко­мая пло­щадь фи­гу­ры равна пло­ща­ди фи­гу­ры, огра­ни­чен­ной гра­фи­ком функ­ции 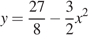и от­рез­ком 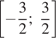оси абс­цисс. Имеем:

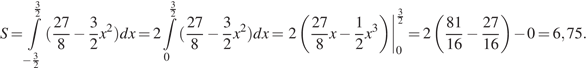
Ответ: 6,75.

Ответ: 6,75

6,75

21. B 14 № 39213. Ве­ло­си­пе­дист вы­ехал с по­сто­ян­ной ско­ро­стью из го­ро­да А в город В, рас­сто­я­ние между ко­то­ры­ми равно 180 км. На сле­ду­ю­щий день он от­пра­вил­ся об­рат­но в А со ско­ро­стью на 8 км/ч боль­ше преж­ней. По до­ро­ге он сде­лал оста­нов­ку на 8 часов. В ре­зуль­та­те ве­ло­си­пе­дист за­тра­тил на об­рат­ный путь столь­ко же вре­ме­ни, сколь­ко на путь из А в В. Най­ди­те ско­рость ве­ло­си­пе­ди­ста на пути из В в А. Ответ дайте в км/ч.

Ре­ше­ние.

Пусть км/ч — ско­рость ве­ло­си­пе­ди­ста на пути из B в A, тогда ско­рость ве­ло­си­пе­ди­ста на пути из A в B равна км/ч. Сде­лав на об­рат­ном пути оста­нов­ку на 8 часов, ве­ло­си­пе­дист за­тра­тил на об­рат­ный путь столь­ко же вре­ме­ни, сколь­ко на путь из A в B, от­сю­да имеем:

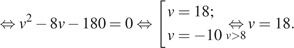
Таким об­ра­зом, ско­рость ве­ло­си­пе­ди­ста была равна 18 км/ч.

Ответ: 18.

Ответ: 18

22. B 14 № 118555. Пер­вый насос на­пол­ня­ет бак за 19 минут, вто­рой — за 57 минут, а тре­тий — за 1 час 16 минут. За сколь­ко минут на­пол­нят бак три на­со­са, ра­бо­тая од­но­вре­мен­но?

Ре­ше­ние.

Обо­зна­чим объем бака за 1. Тогда три на­со­са, ра­бо­тая вме­сте, за­пол­нят бак за

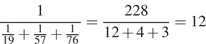минут.

Ответ: 12.

Ответ: 12

23. B 14 № 114647. Из пунк­та A кру­го­вой трас­сы вы­ехал ве­ло­си­пе­дист, а через 50 минут сле­дом за ним от­пра­вил­ся мо­то­цик­лист. Через 5 минут после от­прав­ле­ния он до­гнал ве­ло­си­пе­ди­ста в пер­вый раз, а еще через 30 минут после этого до­гнал его во вто­рой раз. Най­ди­те ско­рость мо­то­цик­ли­ста, если длина трас­сы равна 50 км. Ответ дайте в км/ч.

Ре­ше­ние.

К мо­мен­ту пер­во­го об­го­на мо­то­цик­лист за 5 минут про­ехал столь­ко же, сколь­ко ве­ло­си­пе­дист за 55 минут, сле­до­ва­тель­но, его ско­рость в 11 раз боль­ше. По­это­му, если ско­рость ве­ло­си­пе­ди­ста при­нять за x км/час, то ско­рость мо­то­цик­ли­ста будет равна 11x, а ско­рость их сбли­же­ния — 10 x км/час.

C дру­гой сто­ро­ны, вто­рой раз мо­то­цик­лист до­гнал ве­ло­си­пе­ди­ста за 30 минут, за это время он про­ехал на 50 км боль­ше. Сле­до­ва­тель­но, ско­рость их сбли­же­ния со­став­лят 100 км/час.

Итак, 10 х = 100 км/час, от­ку­да ско­рость ве­ло­си­пе­ди­ста равна 10 км/час, а ско­рость мо­то­цик­ли­ста равна 110 км/час.

При­ме­ча­ние.

В усло­вии явно не ука­за­но, успе­ва­ет ли ве­ло­си­пе­дист про­ехать пол­ный круг до того как мо­то­цик­лист начнёт своё дви­же­ние или нет. Ра­зум­но пред­по­ло­жить, что ве­ло­си­пе­дист не успе­ва­ет про­ехать пол­ный круг, по­то­му что иначе его ско­рость долж­на со­став­лять 1 км/мин, или 60 км/час, что для ве­ло­си­пе­ди­ста труд­но­до­сти­жи­мо.

Ответ: 110

24. B 14 № 504259. Пер­вый и вто­рой на­со­сы на­пол­ня­ют бас­сейн за 10 минут, вто­рой и тре­тий — за 15 минут, а пер­вый и тре­тий — за 24 ми­ну­ты. За сколь­ко минут три эти на­со­са за­пол­нят бас­сейн, ра­бо­тая вме­сте?

Ре­ше­ние.

За одну ми­ну­ту пер­вый и вто­рой на­со­сы за­пол­нят 1/10 бас­сей­на, вто­рой и тре­тий — 1/15 бас­сей­на, а пер­вый и тре­тий — 1/24 бас­сей­на. Ра­бо­тая вме­сте, за одну ми­ну­ту два пер­вых, два вто­рых и два тре­тьих на­со­са за­пол­нят

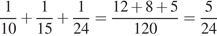бас­сей­на.

Тем самым, они могли бы за­пол­нить 5 бас­сей­нов за 24 ми­ну­ты. По­сколь­ку каж­дый из на­со­сов был учтен два раза, в ре­аль­но­сти пер­вый, вто­рой и тре­тий на­со­сы, ра­бо­тая вме­сте, могут за­пол­нить 5 бас­сей­нов за 48 минут. Зна­чит один бас­сейн они за­пол­нят за 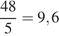минут

Ответ: 9,6.

Ответ: 9,6

9,6

25. B 14 № 26597. Пер­вая труба про­пус­ка­ет на 1 литр воды в ми­ну­ту мень­ше, чем вто­рая. Сколь­ко лит­ров воды в ми­ну­ту про­пус­ка­ет пер­вая труба, если ре­зер­ву­ар объ­е­мом 110 лит­ров она за­пол­ня­ет на 1 ми­ну­ту доль­ше, чем вто­рая труба?

Ре­ше­ние.

Обо­зна­чим — ко­ли­че­ство лит­ров воды, про­пус­ка­е­мой пер­вой тру­бой в ми­ну­ту, тогда вто­рая труба про­пус­ка­ет лит­ров воды в ми­ну­ту. Ре­зер­ву­ар объ­е­мом 110 лит­ров пер­вая труба за­пол­ня­ет на 1 ми­ну­ту доль­ше, чем вто­рая труба, от­сю­да имеем:

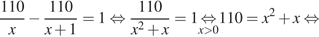
Таким об­ра­зом, пер­вая труба про­пус­ка­ет 10 лит­ров воды в ми­ну­ту.

Ответ: 10.

Ответ: 10

26. B 14 № 39695. Заказ на 380 де­та­лей пер­вый ра­бо­чий вы­пол­ня­ет на 1 час быст­рее, чем вто­рой. Сколь­ко де­та­лей в час де­ла­ет пер­вый ра­бо­чий, если из­вест­но, что он за час де­ла­ет на 1 де­таль боль­ше?

Ре­ше­ние.

Обо­зна­чим — число де­та­лей, ко­то­рые из­го­тав­ли­ва­ет за час пер­вый ра­бо­чий, тогда вто­рой ра­бо­чий за час из­го­тав­ли­ва­ет де­та­лей, 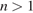. На из­го­тов­ле­ние 380 де­та­лей пер­вый ра­бо­чий тра­тит на 1 час мень­ше, чем вто­рой ра­бо­чий, от­сю­да имеем:

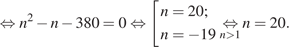
Ответ: 20.

Ответ: 20

27. B 14 № 26585. Мо­тор­ная лодка про­шла про­тив те­че­ния реки 112 км и вер­ну­лась в пункт от­прав­ле­ния, за­тра­тив на об­рат­ный путь на 6 часов мень­ше. Най­ди­те ско­рость те­че­ния, если ско­рость лодки в не­по­движ­ной воде равна 11 км/ч. Ответ дайте в км/ч.

Ре­ше­ние.

Пусть км/ч – ско­рость те­че­ния реки, тогда ско­рость лодки по те­че­нию равна км/ч, а ско­рость лодки про­тив те­че­ния равна км/ч. На об­рат­ный путь лодка за­тра­ти­ла на 6 часов мень­ше, от­сю­да имеем:

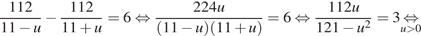
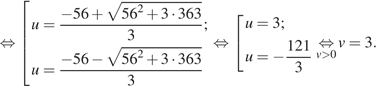
Таким об­ра­зом, ско­рость те­че­ния реки равна 3 км/ч.

Ответ: 3.

Ответ: 3

28. B 14 № 99567. Че­ты­ре ру­баш­ки де­шев­ле курт­ки на 8%. На сколь­ко про­цен­тов пять ру­ба­шек до­ро­же курт­ки?

Ре­ше­ние.

Сто­и­мость че­ты­рех ру­ба­шек со­став­ля­ет 92% сто­и­мо­сти курт­ки. Зна­чит, сто­и­мость одной ру­баш­ки со­став­ля­ет 23% сто­и­мо­сти курт­ки. По­это­му сто­и­мость пяти ру­ба­шек со­став­ля­ет 115% сто­и­мо­сти курт­ки. Это пре­вы­ша­ет сто­и­мость курт­ки на 15%.

Ответ: 15.

Ответ: 15

29. B 14 № 99566. В по­не­дель­ник акции ком­па­нии по­до­ро­жа­ли на не­ко­то­рое ко­ли­че­ство про­цен­тов, а во втор­ник по­де­ше­ве­ли на то же самое ко­ли­че­ство про­цен­тов. В ре­зуль­та­те они стали сто­ить на 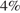де­шев­ле, чем при от­кры­тии тор­гов в по­не­дель­ник. На сколь­ко про­цен­тов по­до­ро­жа­ли акции ком­па­нии в по­не­дель­ник?

Ре­ше­ние.

Обо­зна­чим пер­во­на­чаль­ную сто­и­мость акций за 1. Пусть в по­не­дель­ник акции ком­па­нии по­до­ро­жа­ли на , и их сто­и­мость стала со­став­лять 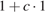. Во втор­ник акции по­де­ше­ве­ли на , и их сто­и­мость стала со­став­лять 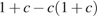. В ре­зуль­та­те они стали сто­ить на 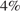де­шев­ле, чем при от­кры­тии тор­гов в по­не­дель­ник, то есть 0,96. Таким об­ра­зом,