Сложение взаимно-перпендикулярных колебаний

Материальная точка может совершать колебания вдоль оси х, так и вдоль оси у. В данном случае колебания проходят во взаимно перпендикулярных направлениях.Для простоты начало отсчета выбирается так, чтобы начальная фаза первого колебания была равна нулю.

Запишем уравнение гармонических колебаний, которые можно представить в виде системы

, (19.26)

Разность фаз обоих колебаний равна φ. А и В – амплитуды складываемых колебаний. Уравнение траектории результирующего колебания находится исключением из выражений (19.26) параметра t

(19.27)

сделаем замену .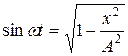

После несложных преобразований подставляя (19.27) в (19.26) получим уравнение эллипса.

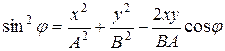. (19.28)

Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.

Ориентация осей эллипса зависит от разности фаз φ, и амплитуд А и В складываемых колебаний.

Определим траекторию для некоторых частных случаев:

1) (m = 0,±1, ±2…) – в данном случае эллипс вырождается в отрезок прямой, такие колебания называются линейно поляризованные (Примеры траектории движения для различных разностей фаз и соотношения частот показаны на рис.19.6)

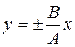. (19.29)

2) (m = 0,±1, ±2…) В данном случае уравнение имеет вид

. (19.30)

При условии А=В то эллипс (19.30) вырождается в уравнение окружности. Такие колебания называют циркулярно поляризованными или колебаниями, поляризованными по кругу.

Если частоты, складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания сложная. Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Форма фигур Лиссажу зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний, как показано на рис. 19.6 (вторая строка). Анализ фигур Лиссажу – широко используемый метод исследования соотношений частот, разности фаз складываемых колебаний, а также формы колебаний.

X:Y	φ=0	φ=π/4	φ= π/2	φ= 3π/4	φ= π
1:1
1:2
Рис.19.6.