Теорема Гаусса

17.1 Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная

, (17.1)

где 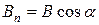— проекция вектора на направление нормали к площадке dS (a — угол между векторам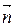и и ), — вектор, модуль которого равен dS, а направление совпадает с направлением нормали 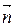к площадке. Поток вектора может быть как положительным, так и отрицательным в зависимости от знака соs a (определяется выбором положительного направления нормали 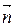). Обычно поток вектора связывают с определенным контуром, по которому течет ток. В таком случае положительное направление нормали к контуру нами уже определено: оно связывается с током правилом правого винта. Таким образом, магнитный поток, создаваемый контуром через поверхность, ограниченую им самим, всегда положителен.

Поток вектора магнитной индукции через произвольную поверхность

. (17.2)

Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору , и

.

Из этой формулы определяется единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, проходящий через плоскую поверхность площадью 1 м², расположенную перпендикулярно однородному магнитному полю, индукция которого 1 Тл (1 Вб=1 Тл×м²).

Теорема Гаусса для поля : поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

.

Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

В качестве примера рассчитаем поток вектора через соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью m, равна

.

Магнитный поток через один виток соленоида площадью S равен

,

а полный магнитный поток, сцепленный со всеми витками соленоида и называемый потокосцеплением,

.

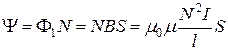Обобщая результаты своих многочисленных опытов, Фарадей пришел к количественному закону электромагнитной индукции e_i. Он показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Значение индукционного тока, а следовательно, и э.д.с. электромагнитной индукции e_i, определяются только скоростью изменения магнитного потока, т.е.

e_i . (17.3)

Теперь необходимо выяснить знак e_i. Знак магнитного потока зависит от выбора положительной нормали к контуру. В свою очередь, положительное направление нормали связано с током правилом правого винта. Следовательно, выбирая определенное положительное направление нормали, мы определяем как знак потока магнитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими представлениями и выводами, можно соответственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре э.д.с.

e_i 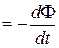. (17.4)

Знак минус показывает, что увеличение потока называется э.д.с. e_i < 0, т.е. поле индукционного тока направлено навстречу потоку; уменьшение потока 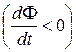вызывает e_i > 0, т.е. направления потока и поля индукционного тока совпадают. Знак минус в формуле (17.4) является математическим выражением правила Ленца — общего правила для нахождения направления индукционного тока.

Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного по тока, вызвавшего этот индукционный ток.

Закон Фарадея может быть непосредственно получен из закона сохранения энергии. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное плоскости контура, и может свободно перемещаться. Под действием силы Ампера , направление которой показано на рисунке, проводник перемещается на отрезок . Эта сила совершает работу . Произведение , а , таким образом, сила Ампера производит работу dA = I d F, где d F — пересеченный проводником магнитный поток.

Если полное сопротивление контура равно 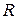, то, согласно закону сохранения энергии, работа источника тока за время 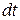равная (eIdt) будет складываться из работы на джоулеву теплоту и работы по перемещению проводника в магнитном поле :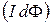

e ,

откуда ,

где ℰ_i есть закон Фарадея.