 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Момент инерции. При изучении вращения твердого тела пользуются понятием момента инерции
|
|
При изучении вращения твердого тела пользуются понятием момента инерции. Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:
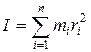 . (4.5)
. (4.5)
В случае непрерывного распределения масс эта сумма сводится к интегралу
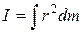 , (4.6)
, (4.6)
где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с координатами х, у, z. 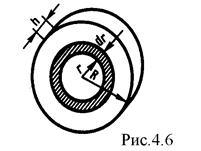
В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис.4.6). Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r + dr. Момент инерции каждого полого цилиндра dI = r 2 dm (так как dr < < r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm - масса всего элементарного цилиндра; его объем 2 πrh dr. Если ρ - плотность материала, то dm = ρ· 2 πrh dr и dI = 2 π ρhπr3dr. Тогда момент инерции сплошного цилиндра
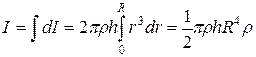 ,
,
но так как π R 2 h - объем цилиндра, то его масса m = π R 2 hρ, а момент инерции
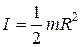 .
.
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела I относительно любой оси вращения О равен моменту его инерции IC относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния a 2 между осями:
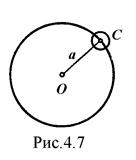 I = IC + ma 2. (4.7)
I = IC + ma 2. (4.7)
Приведем значения моментов инерции (табл.1) для некоторых тел (тела считаются однородными, m - масса тела).
| Таблица 1 | ||
| Тело | Положение оси вращения | Момент инерции |
| Полый тонкостенный цилиндр радиусом R | Ось симметрии | mR 2 |
| Сплошной цилиндр или диск радиусом R | То же | 1/2 mR 2 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | 1/12 ml 2 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | 1/3 ml 2 |
| Шар радиусом R | Ось проходит через центр шара | 2/5 mR 2 |
Дата публикования: 2014-10-04; Прочитано: 1055 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
