Линейное уравнение первого порядка

Решить линейное дифференциальное уравнение первого порядка можно с помощью введения двух новых искомых функций и 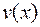, положив 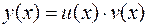, и дополнительного условия на одну из них, выби­раемую произвольно. Рассмотрим применение этого метода на следующем примере.

Пример4. Решить дифференциальное уравнение .

Решение. Будем искать решение в виде: ;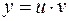

Тогда ; Подставляя выражения для искомой функции и ее производной в рассматриваемое дифференциальное уравнение, получим:

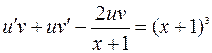, или

. (7)

Поскольку одну из функци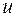й и мы вправе выбрать произвольно, выберем ее так, чтобы выполнялось условие: Тогда уравнение (7) запишется в виде: 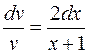. Это уравнение легко интегрируется: ; .

Произвольную постоянную здесь можно положить равной нулю, так как мы выбираем частное решение. Тогда .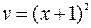

После подстановки в исходное уравнение получим (при ):

; ; .

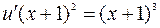Таким образом, искомое общее решение.