Свойства векторного произведения

Все свойства векторного произведения можно условно разбить на две группы.

I. Алгебраические свойства.

1) Антикоммутативность: .{ Первые два условия определения не зависят

от порядка векторов, но тройки a, b, 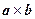и b, a, 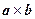ориентированы противоположно (§9)}

2) {Доказать самим}

3) 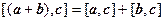{б/д}

II. Геометрические свойства.

1) − равенство нулю векторного произведения является необходимым и достаточным условием коллинеарности. { Доказать самим }

2) − площадь параллелограмма, построенного на двух векторах равна модулю векторного произведения этих векторов. {Очевидно}

Для вывода координатной формы векторного произведения поступим так же, как и в случае скалярного: .

Здесь уже использованы соотношения: и т.д.

Легко заметить, что формула векторного произведения может быть записана в виде символического определителя: .

Пример. Вычислить S_∆ABC, если даны тт. А (1,2,0), В (3,0,−3), С (5,2,6).

{ }

§11. Смешанное произведение трех векторов.

Определение. Смешанным произведением векторов a, b и c называется число, равное