Теорема Жегалкина

Каждая функция из 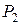может быть представлена в виде полинома Жегалкина единственным образом.

Здесь единственность понимается с точностью до порядка слагаемых в сумме и порядка сомножителей в конъюнкциях:

, s = 0, 1,..., n.

Доказательство. Любая функция из Р ₂ может быть представлена формулой над { x ₁ & x ₂, x ₁Å x ₂, 0, 1}, а эта формула после раскрытия всех скобок и приведения подобных членов дает полином Жегалкина. Докажем единственность представления. Рассмотрим функции f (x ₁,..., x_n) от n переменных. Мы знаем, что всего таких функций, т.е. их таблиц истинности, 2 ⁿ. Подсчитаем число различных полиномов Жегалкина от n переменных, т.е. число вариаций вида: . Число наборов равно числу всех подмножеств множества { x ₁,..., x_n }, сюда входит и пустое множество (если s = 0). Число подмножеств множества из n элементов равно 2 ⁿ, а так как каждый набор входит с коэффициентом , принимающим два значения: 0 или 1, то число всевозможных полиномов будет . Так как каждому полиному соответствует единственная функция, число функций от n переменных равно числу полиномов, то каждой функции будет соответствовать единственный полином.

Определение. Функция f (x ₁,..., x_n), полином Жегалкина для которой имеет следующий линейный относительно переменных вид: f = а ₀ Å а ₁ х ₁ Å а ₂ х ₂ Å... Å а_nх_n, называется линейной.

Лемма о нелинейной функции. Суперпозицией нелинейной функции, отрицания и константы 1 можно получить конъюнкцию.

Доказательство. Пусть f (x ₁,..., x_n) – нелинейная функция. Тогда полином Жегалкина содержит для нее слагаемое, в котором присутствует произведение x_ix_j. Будем считать для простоты, что x ₁ x ₂ в многочлене Жегалкина является этим произведением. Произведя группировку слагаемых, функцию f представим в виде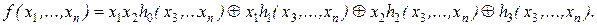

Функция h ₀ не есть тождественный нуль, иначе в полиноме Жегалкина отсутствует слагаемое с произведением x ₁ x ₂. Тогда существует набор (a ₃, …, a_n) из 0 и 1, для которого h ₀(a ₃, …, a_n) = 1. Пусть h ₁ (a ₃, …, a_n) = a, h ₂(a ₃, …, a_n) = b, h ₃(a ₃, …, a_n) = c. Тогда

Построим функцию:

где d = ab Å c. Если d = 0, то h (x ₁, x ₂) = x ₁ x ₂. Если d = 1, то h (x ₁, x ₂) = x ₁ x ₂ Å 1 и тогда Лемма доказана.

Функция f (x ₁,..., x _n) сохраняет константу a Î {0, 1}, если f (a, …, a) = a.

Пример 4. Функция xy сохраняет 0, сохраняет 1. Функция x ® y сохраняет 1 и не сохраняет 0.

2.4.6. Замыкание и замкнутые классы

Определение 1. Пусть M Í Р ₂. Замыканием М называется множество всех функций из P ₂, которые можно выразить формулами над М. Замыкание М обозначается [ M ].

Определение 2. Множество функций М называется замкнутым классом, если [ M ]= M.

Пример 1.

1) P ₂ – замкнутый класс.

2) Множество {1, x ₁Å x ₂} не является замкнутым классом. Его замыканием будет класс линейных функций: [{1, x ₁ Å x ₂}] = { f (x ₁,..., x_n) = c ₀ Å c ₁ x ₁ Å... Å c_nx_n }. Действительно, по определению формулы над М, функция f (G ₁, x ₃), где f – есть сумма по модулю 2, G ₁ – функция х ₁ Å х ₂, будет формулой над М: f (G ₁, x ₃) = (x ₁ Å x ₂) Å x ₃.

З амечание. В терминах замыкания и замкнутого класса можно дать другое определение полноты, эквивалентное исходному:

М – полная система, если [ M ] = P ₂.

3) A = { f (x ₁,..., x_n)| f (1, 1,..., 1) = 0} – незамкнутый класс. Возьмем формулу над этим множеством. Пусть f, g ₁,..., g_n Î A, т.е. f (1, 1,..., 1) = 0, g ₁(1, 1,..., 1) = 0, тогда f (g ₁,..., g_n) Î [ A ]. Посмотрим, принадлежит ли функция f (g ₁,..., g_n) множеству А. f (g ₁(1,..., 1), g ₂(1,..., 1),..., g_n (1,..., 1) = f (0,..., 0)), но f (0,..., 0) не обязано быть равным 0. Действительно, пусть g ₁(x ₁, x ₂) = x ₁ Å x ₂, g ₂(x) = x Î A. Возьмем g ₂(g ₁(x ₁, x ₂)) = x ₁ Å x ₂ Î [ A ], g ₂(g ₁(1, 1)) = 1 Å 1 = 0, следовательно, g ₂(g ₁(x ₁, x ₂)) Ï A, отсюда [ A ] ¹ A и А – незамкнутый класс.

Важнейшие замкнутые классы в Р ₂

1) Т₀ - класс функций, сохраняющих константу 0.

Т ₀ = { f (x ₁,..., x_n)| f (0,..., 0) = 0, n = 1, 2,...}. Покажем, что Т ₀ является собственным подмножеством Р ₂, т.е. Т ₀ ¹ Æ и Т ₀ Ì Р (не совпадает с Р ₂). Для этого достаточно привести примеры функций, входящих в Т ₀, и примеры функций из Р₂, не входящих в Т ₀: x ₁& x ₂, x ₁Ú x ₂, x Î Т ₀ и x ₁| x ₂, x ₁ x ₂, Ï Т ₀. Покажем далее, что [ Т ₀] = Т ₀. Вложение Т ₀ Í [ Т ₀] очевидно, так как по определению формулы любая функция из Т ₀ является формулой над Т ₀ и, следовательно, принадлежит [ Т ₀]. Покажем, что [ Т ₀]Í Т ₀. Для этого надо показать, что Ф = f (f ₁,..., f_m) Î [ Т ₀], если все функции f, f ₁, f ₂, f ₃,..., f _m Î Т ₀. Надо заметить, что в формуле в качестве функции f ₁ могут быть взяты переменные, которые мы договорились считать тождественными функциями. Тождественная функция принадлежит классу Т ₀, поэтому достаточно показать, что Ф = f (f ₁,..., f_m) Î Т ₀. Для этого рассмотрим следующую функцию: Ф (0,..., 0) = f (f ₁(0,..., 0), f ₂(0,..., 0),...) = f (0,..., 0) = 0.

Число функций, зависящих от n переменных и принадлежащих Т ₀, будет равно

2) T ₁ – класс функций, сохраняющих константу 1.

T ₁ = { f (x ₁,...) | f (1, 1,...) = 1}; x ₁& x ₂, x ₁Ú x ₂, x Î T ₁, х ₁Å х ₂, x ₁ x ₂Ï T ₁, следовательно Т ₁ – собственное подмножество Р ₂.

Покажем, что [ T ₁] Í T ₁, обратное включение следует из определения формулы и замыкания. Так как тождественная функция входит в Т ₁, можно рассмотреть Ф = f (f ₁,..., f_n) Î [ T ₁], где f, f ₁,..., f_n Î T ₁. Найдем Ф (1,..., 1) = f (f ₁(1,..., 1),..., f_n (1,..., 1)) = f (1,..., 1) = 1, следовательно, Ф = f (f ₁,..., f_n) Î T ₁, отсюда следует [ T ₁] = T ₁.

3) S – класс самодвойственных функций.

S = { f (x ₁,...)| f * = f }; x, , x ₁Å x ₂Å x ₃Î S, x ₁& x ₂, x ₁Ú x ₂, x ₁Å x ₂Ï S, следовательно, S – собственное подмножество Р ₂. | S (n)| = . Покажем, что [ S ]Í S. Ф = f (f ₁,..., f_n) Î [ S ], если f, f ₁,..., f_n Î S, а также, что Ф Î S. По принципу двойственности, Ф * = f *(f ₁*,..., f_n *) = f (f ₁,..., f_n) = Ф, отсюда S – замкнутый класс.

4) L – класс линейных функций.

L = { f (x ₁,...)| f = c ₀Å c ₁ x ₁Å...Å c_nx_n }; очевидно, L ¹ Æ, с другой стороны

L ¹ P ₂, так как x ₁& x ₂ Ï L. Заметим, что тождественная функция принадлежит L и | L (n)| = 2 ^{n +1}. Покажем, что [ L ] Í L. Рассмотрим Ф = f (f ₁,..., f_m), где f, f ₁,..., f_n Î L. Тогда Ф = а ₀ Å а ₁(с ₁₀ Å с ₁₁ х ₁ Å...Å c _{1 n}x_{n 1}) Å a ₂(c ₂₀ Å c ₂₁ x ₁ Å c ₂₂ x ₂Å...Å c _{2 n}x_{n 2})Å...Å a_n (c_{m 0} Å c_{m 1}x₁ Å... Å c_mnx_nm) = в ₀ Å в ₁ х ₁ Å...Å в_nх_n Þ Ф Î L.

5) М – класс монотонных функций.

Определение. Набор a ' = (a ₁,..., a_n) предшествует набору b ' = (b ₁,..., b_n) и это обозначается a ' Ð b ', если для 1£ i £ n a_i £ b_i, например: a '= (0010), b ' = (0110), тогда a ' Ð b '. Не любые два набора находятся в отношении предшествования, например, наборы (0110) и (1010) в таком отношении не находятся. Отношение предшествования () является отношением порядка на множестве наборов длины n, множество таких наборов будет частично упорядоченным множеством по отношению к операции.

Определение. Функция f (x ₁,..., x_n) называется монотонной, если для двух наборов a ' и b ', таких что a ' Ð b ', выполняется f (a ') £ f (b '). Функции 0, 1, x, x ₁& x ₂, x ₁Ú x ₂ Î M, x ₁¯ x ₂, x ₁Å x ₂, x ₁~ x ₂ Ï M.

Для числа монотонных функций, зависящих от n переменных, существуют оценки сверху и снизу, но точное число сосчитать не удается. Покажем, что М замкнутый класс. Рассмотрим функцию Ф Î[ M ], Ф = f (f ₁,..., f_m), где f, f ₁,..., f_m Î M, причем можем считать, что все они зависят от n переменных. Пусть набор a ' = (a ₁,..., a_n), b ' = (b ₁,..., b_n). Рассмотрим Ф (a ₁,..., a_n) = f (f ₁(a ₁,..., a_n), …, f_m (a ₁,..., a_n)) и Ф (b ₁,..., b_n) = f (f ₁(b ₁,..., b_n),..., f_m (b ₁,..., b_n)). Здесь f ₁(a) Ð f ₁(b),..., f_m (a) Ð f_m (b), тогда набор (f ₁(a),..., f_m (a)) Ð (f ₁(b),..., f_m (b)), но тогда Ф (a ') Ð Ф (b '), так как f Î M, отсюда Ф = f (f ₁,...,) – монотонная функция.

Определение. Функция f есть суперпозиция над M, если f реализуется некоторой формулой над M.

Лемма о немонотонной функции. Отрицание можно получить суперпозицией констант 0 и 1, тождественной функции и немонотонной функции.

Доказательство. Пусть f (x ₁,..., x_n) – немонотонная функция. Тогда существуют наборы и , для которых но Пусть i ₁, …, i_k есть все те номера аргументов, для которых , p =1, …, k. На всех остальных аргументных местах j имеем a_j = b_j. В выражении 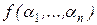заменим нули на местах i ₁, …, i_k на x. В результате получим функцию g (x), для которой g (0) = f () = 1 и g (1) = f (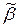) = 0. Функция g (x) является отрицанием.

Классы T ₀, T ₁, L, S, M пересекаются, но не совпадают, что видно из следующей таблицы, где «+» означает, что функция принадлежит данному классу и «-» – не принадлежит.

	T 0	T 1	L	S	M
x	+	+	+	+	+
	-	-	+	+	-
	+	-	+	-	+
	-	+	+	-	+
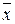
x 1 x 2	+	+	-	-	+

A ={ x, 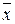, 0, 1, x ₁ x ₂) не является полной системой функций так как всегда есть функции Î Р ₂ не входящие в эти классы.

Задачи

1. Доказать, что пересечение любых двух замкнутых классов замкнуто.

2. Доказать, что объединение двух замкнутых классов не всегда замкнуто.