Імпульсна модуляція

У розглянутих вище видах модуляції як переносник використовувалося гармонійне коливання. Однак як переносник можна використовувати й інші коливання, у тому числі і періодичній послідовності коротких прямокутних імпульсів. Це випливає з розглянутої нижче теореми Котельникова, відповідно до якої функцію, що має обмежений спектр, можна цілком охарактеризувати її миттєвими значеннями, узятими через інтервал години (інтервал дискретизації)

, (7.5.1)

де f_в – найвища частота в спектрі сигналу.

При використанні як переносник періодичної послідовності прямокутних імпульсів можливі наступні види імпульсної модуляції: по амплітуді (АИМ), чи ширині тривалості імпульсів (ШИМ) (мал.7.5.1), по частоті (ЧИМ) і фазі (ФИМ).

Немодульована послідовність імпульсів представляється рядом Фур'є. Для одержання спектра сигналу при імпульсній модуляції в цьому випадку необхідно підставити відповідне вираження модулююмого параметра. Як приклад розглянемо амплітудно-імпульсну модуляцію (АИМ) чистим тоном. У цьому випадку за законом керуючого сигналу змінюється амплітуда і, отже, площа імпульсів:

. (7.5.2)

Частоту називають частотою дискретизації.

Рис. 7.5.1.

Підставивши це вираження в (6.15), одержимо

. (7.5.3)

де .

Після тригонометричних перетворень знаходимо

(7.5.4)

Рис. 7.5.2.

Спектр цього коливання показаний на мал.7.5.2. Порівнюючи його зі спектром звичайної АМ, зауважуємо, що при АИМ кожна частотна складова (гармоніка) немодульованої послідовності імпульсів модулюється незалежно як ізольована "несуча". Це дозволяє здійснювати демодуляцію при АИМ за допомогою фільтра, що пропускає одну з "несучих" c бічними частотами і звичайним амплітудним детектором. Крім того, у спектрі сигналу з АИМ міститься складова низькочастотного сигналу, що модулює, з частотою. Отже демодуляція при АИМ може бути здійснена звичайним фільтром нижніх частот, що пропускають низькочастотне коливання U(t). Однак виділення сигналу, що модулює, при обох випадках детектировання можливо, як це видно з мал.7.5.2 лише при чи .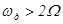

Звичайно на практиці частоту проходження імпульсів беруть рівною

,

де - максимальна частота в спектрі сигналу, що модулює.

Аналогічним образом можна визначити спектри і при інших видах імпульсної модуляції. Через громіздкість розрахунків отут вони не приводяться. Помітимо тільки, що при імпульсних видах модуляції ширина спектра практично не залежить від виду модуляції і визначається в основному тривалістю і формою імпульсів.

8. Дискретизація детермінованих сигналів.

8.1 Розкладання функцій у ряд Котельникова.

Реальні сигнали мають обмежену смугу частот. Такі сигнали мають чудову властивість, уперше установленим В.А.Котельников і вираженим у його теоремі, що грає фундаментальну роль у теорії і техніці зв'язку.

Рис. 8.1.1.

Якщо в загальному випадку безупинна функція години визначається на кінцевому інтервалі незліченною безліччю своїх миттєвих значень (мал.8.1.1.), то функції часу з обмеженим спектром відповідно до теореми Котельникова на кінцевому інтервалу визначаються кінцевою безліччю своїх значень. Відсутність у спектрі функції частот вище деякої граничної накладає визначені обмеження на її зміни в досить малому інтервалі години . Тому через крапки, що відображають миттєві значення функції і узяті через визначений інтервал години друг від друга, можна провести криву одним єдиним способом.

Теорему В.А.Котельникова можна сформулювати в наступному виді:

“Будь-яка функція f(t), спектральна щільність якої відмінна від нуля в смузі частот , цілком визначається послідовністю своїх миттєвих значень, узятих у дискретних крапках через інтервали часу . Значення функції в будь-якій проміжній крапці визначаються вираженням

, (8.1.1)

де 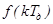- значення безупинної функції в дискретних крапках відсіків .”

Останнє вираження називається рядом Котельникова, коефіцієнти розкладання якого являють собою відсіки функції, а функціями розкладання є так називані функції відсіків типу :

. (8.1.2)

Ці функції мають властивість

(8.1.3)

Таким чином, у момент часу сума ряду (8.1.1) визначається лише k-им членом, всі інші члени ряду в цей момент часу звертаються в нуль. Розкладання функції в ряд Котельникова ілюструється на мал.8.1.2.

Рис. 8.1.2.

Функції відсіків ортогональні на нескінченному інтервалі часу, тобто

(8.1.4)

Енергія сигналу через його відсікові значення виражається в такий спосіб:

. (8.1.5)

Перейдемо тепер до доказу теореми Котельникова.

Нехай спектральна щільність функції f(t)

. (8.1.6)

відмінна від нуля в смузі частот . Тоді для цієї функції

зворотним перетворенням Фур'є одержимо

. (8.1.7)

Спектральну функцію , що не містить періодичних складових на інтервалі , аналогічно (3.11) можна розкласти в ряд Фур'є з періодом :

, (8.1.8)

коефіцієнти якого визначаються вираженням

. (8.1.9)