Частотна модуляція

При частотній модуляції за законом коливання, що модулює, U(t) змінюється частота високочастотного несучого коливання.

На мал.7.2.1 показані графіки що модулює і модульованого сигналів у випадку модуляції чистим тоном. Одержимо аналітичне вираження для Чм-коливання. При модуляції чистим тоном

Рис. 7.2.1.

, (7.2.1)

де - максимальне відхилення частоти, називане девіацією частоти, а 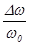- відносна зміна частоти. По своєму визначенню миттєва кругова частота є похідної за годиною від аргументу тригонометричної функції cosy(t), що представляє коливання, тобто

. (7.2.2)

З останнього вираження одержимо

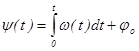, (7.2.3)

тобто фаза коливання визначається інтегралом від кругової частоти. Тому для ЧМ - коливання при модуляції чистим тоном можна записати

(7.2.4)

Зауважуємо, що зміна частоти за законом приводить до зміни фази за законом 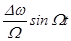. Величина називається індексом частотної модуляції і має сенс максимальної величини (амплітуди) зміни фази при частотній модуляції.

Заміняючи косинус суми двох кутів по відомих формулах тригонометрії, замість (7.2.4) при одержимо

. (7.2.5)

Визначимо тепер спектр частотно-модульованого сигналу. Почнемо з випадку малого індексу модуляції, коли . У цьому випадку

(7.2.6)

. (7.2.7)

Зауважуємо, що при малому індексі модуляції спектр ЧМ - коливання відрізняється від спектра АМ - коливання тільки зрушенням фази нижньої бічної частоти на 180^о. Це ілюструється мал.7.2.2, на якому показана векторна діаграма для ЧМ - коливання (порівняй з мал.7.1.3).

На діаграмі результуючий вектор ОД змінюється як по фазі, так і по амплітуді,однак при 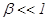амплітудні зміни настільки малі, що ними можна зневажити. При довільних значеннях b с обліком усіх частотних складових спектра результуючий вектор буде змінюватися тільки по фазі.

Визначимо тепер спектр ЧМ - коливання при довільному індексі модуляції. Для цього періодичні функції і 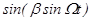розкладемо у виряджай Фур'є, коефіцієнти яких, як доводитися в теорії бесселевих функцій, є функціями Бесселя першого роду:

, (7.2.8)

. (7.2.9)

Підставляючи останні вираження в (7.2.5) і роблячи тригонометричні перетворення, остаточно одержимо

(7.2.10)

Таким чином, ЧМ коливання при модуляції чистим тоном має дискретний спектр і складається з несучої і нескінченного числа бічних частот з амплітудами . Однак практично ширина спектра при частотній модуляції обмежена. Це можна помітити на мал.7.2.3, на якому приведені графіки функцій . При і функції убувають настільки швидко, що ними можна зневажити, тобто вважати, що . Тому ширина спектра при широкополосній ЧМ () буде дорівнює

, (7.2.11)

тобто приблизно дорівнює подвоєної девіації частоти.

Рис. 7.2.4.

На мал.7.2.4 як приклад показань графік модуля спектра ЧМ коливання при = 5.

Таким чином, ширина спектра при широкополосній ЧМ у +1 раз ширше, ніж звичайної АМ. Перевагою частотної модуляції є сталість потужності, тому що амплітуда сигналу в процесі модуляції не змінюється.

Відзначимо тепер, що при частотній модуляції девіації частоти визначається амплітудою сигналу, що модулює, U(t). При зменшенні амплітуди сигналу, що модулює, зменшується індекс модуляції і дійсна ширина 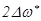спектра. При постійній амплітуді і зміна частоти моделюючого сигналу змінює індекс модуляції, число ліній і інтервал між лініями в спектрі ЧМ коливання, однак ширина спектра 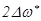практично залишається постійної.

Вище розглядався випадок модуляції чистим тоном. При модуляції складним сигналом спектр ЧМ коливання буде більш богатим, а ширина спектра при буде дорівнює

, (7.2.12)

де - максимальна кругова частота в спектрі сигналу, що модулює.