 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Функцияның дифференциалы
|
|
| Номер изменения | Номера листов | Основание для внесения изменений | Подпись | Расшифровка подписи | Дата | Дата введения изменения | ||
| замененных | новых | аннулированных | ||||||
Функцияның дифференциалы
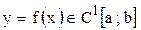 болсын. Онда
болсын. Онда 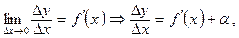 мұндағы
мұндағы 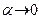 , егер
, егер 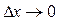 . Бұдан
. Бұдан
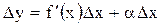 .
.
Анықтама 4. 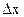 -ке қатысты сызықтық болатын
-ке қатысты сызықтық болатын 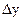 функциясының өсімшесінің негізгі бөлігі функцияның дифференциалы деп аталады және былай белгіленеді:
функциясының өсімшесінің негізгі бөлігі функцияның дифференциалы деп аталады және былай белгіленеді: 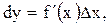
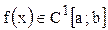 .
.
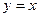 болсын. Онда
болсын. Онда 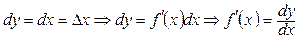 . Функцияның дифференциалының мынадай қасиеттері бар:
. Функцияның дифференциалының мынадай қасиеттері бар:
1. 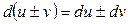
2. 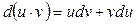
3. 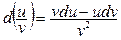
4. 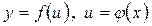 немесе
немесе 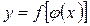 болсын. Онда
болсын. Онда
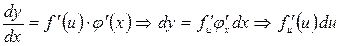 - бірінші дифференциалдың формасының инварианттылық қасиеті.
- бірінші дифференциалдың формасының инварианттылық қасиеті.
5. 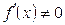 болса,
болса, 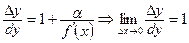 теңдігі орынды болғандықтан, жуықтап есептеуде
теңдігі орынды болғандықтан, жуықтап есептеуде 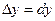 деп алуға болады, немесе
деп алуға болады, немесе
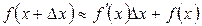 (5)
(5)
Мысал 5. 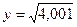 есепте.
есепте.
Шешуі: 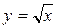 функциясын қарастыралық және
функциясын қарастыралық және 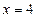 деп алайық.
деп алайық. 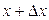 ретінде
ретінде 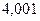 санын аламыз. Онда
санын аламыз. Онда 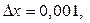
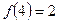 .
.
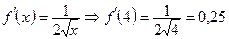 . Онда (5)-тен
. Онда (5)-тен 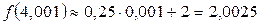 .
.
Дата публикования: 2014-10-19; Прочитано: 3203 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
