Методы решения систем линейных уравнений

Формулы Крамера используются для решения системы, основная матрица которой квадратная, невырожденная ( ). Названные формулы имеют вид:

(2.12)

где − главный определитель системы, т. е.

(2.13)

− определители, полученные из определителя заменой в нем j -го столбца

столбцом свободных членов, т. е.

; ,…;

,…; .

Пример 8. Решить систему по формулам Крамера и сделать проверку.

Решение.

Основная матрица системы невырожденная, так как 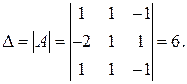Определители 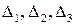соответственно таковы:

; ; .

Применяя формулы Крамера, находим неизвестные:

Подставляя найденные значения неизвестных в каждое уравнение системы, получаем верные равенства: 2 = 2, 3 = 3, 6 = 6.

Метод Гаусса (метод последовательного исключения неизвестных) используется для решения систем линейных уравнений произвольного вида, т. е. для случаев, когда и

Введем элементарные преобразования ЛСУ, которые приводят к эквивалентной системе, т. е. к системе, которая имеет такие же решения, что и исходная. К элементарным преобразованиям относятся:

1) умножение любого уравнения системы на число, отличное от нуля;

2) перестановка двух любых уравнений системы;

3) сложение одного уравнения системы с любым другим, умноженным на

произвольное число;

4) перенумерация неизвестных.

Очевидно, что элементарные преобразования системы соответствуют элементарным преобразованиям над строками расширенной матрицы 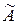этой системы. Перенумерация неизвестных соответствует перестановке столбцов основной матрицы А.

Если r = n, то с помощью указанных элементарных преобразований расширенная матрица 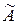и система приводятся к треугольному виду (прямой ход метода Гаусса):

(2.14)

причем

Из последнего уравнения системы (2.14) определяется . Подставляя найденное в предпоследнее уравнение системы (2.14), находим . Через n шагов определяются все неизвестные системы (обратный ход метода Гаусса).

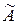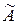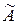Если , то с помощью элементарных преобразований приводится к трапециевидной матрице того же размера, что и , в ней m строк, из них ( – нулевые, и () столбец, т. е. матрица принимает вид:

, (2.15)

причем

По полученной матрице (2.15) восстанавливается ЛСУ:

(2.16)

в которой r уравнений и n неизвестных. Полученная система (2.16), как и исходная, совместная, но неопределенная, т. е. имеет бесчисленное множество решений. Чтобы найти эти решения, перепишем систему уравнений (2.16) в виде:

(2.17)

Неизвестные 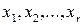называются базисными, коэффициенты при них образуют минор r -го порядка, отличный от нуля (базисный минор). Неизвестные называются свободными. Придавая свободным неизвестным произвольные значения, соответственно , найдем базисные неизвестные: − из последнего уравнения полученной системы (2.17); 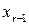− из предпоследнего и, наконец, через r шагов − − из первого уравнения системы (2.17).

Пример 10. Дана система линейных уравнений:

Требуется: 1) записать расширенную матрицу системы и привести ее к трапециевидной форме; 2) определить ранги основной и расширенной матриц системы и сделать вывод о совместности системы; 3) в случае, если система совместна, восстановить по трапециевидной расширенной матрице систему уравнений, эквивалентную исходной, и решить ее методом Гаусса; 4) сделать проверку решения.

Решение.

1) Запишем матрицу 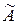и с помощью элементарных преобразований приведем ее к трапециевидной форме:

~ ~ ~

~ .

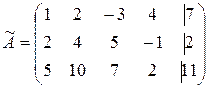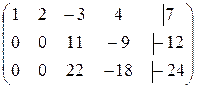2) Ранг основной матрицы равен двум, так как ее базисный минор

а все миноры третьего порядка равны нулю. Ранг расширенной матрицы также равен двум, так как и для нее все миноры третьего порядка, уже с учетом столбца свободных членов, равны нулю. Следовательно, система совместна.

3) Восстановим по трапециевидной расширенной матрице систему уравнений, учитывая, что на последнем шаге преобразований пришлось переставлять второй и третий столбцы:

В системе четыре неизвестных, а ранг равен двум, следовательно, система имеет бесчисленное множество решений и два неизвестных являются свободными (). Выбираем в качестве базисных неизвестных , , тогда будут свободными неизвестными. Перепишем систему в виде:

(2.18)

Пусть , где – любые числа, тогда из последнего уравнения системы (2.12) получаем: . Подставляя найденное в первое уравнение системы (2.12), находим .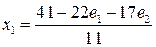

4) Для проверки подставляем найденные значения в исходную систему уравнений и получаем верные равенства:

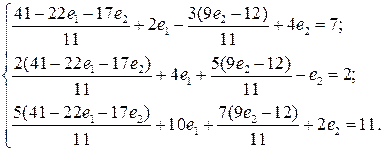
Следовательно, множество решений системы имеет вид:

.