 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Операции над матрицами. Суммой матриц и называется такая матрица ,
|
|
Суммой матриц 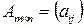 и
и  называется такая матрица
называется такая матрица  ,
,
элементы которой равны сумме соответствующих элементов матриц A и B, т. е.
 (1.19)
(1.19)
Складывать можно только матрицы одинакового размера.
Произведением числа  на матрицу
на матрицу  называется такая матрица
называется такая матрица  ,
,
элементы которой вычисляются по формуле:
 (1.20)
(1.20)
Матрица  называется противоположной матрице
называется противоположной матрице 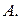
Разность матриц 
 можно определить так:
можно определить так: 
Операции сложения матриц и умножения матрицы на число удовлетворяют следующим свойствам:
1)  5)
5) 
2)  6)
6) 
3)  7)
7) 

4)  8)
8) 
где  матрицы;
матрицы;  числа.
числа.
Пример 3. Даны матрицы  ;
;  . Вычислить матрицу
. Вычислить матрицу 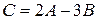 .
.
Решение.

 .
.
Операция умножения матрицы А на матрицу В возможна только тогда,
когда число столбцов первой матрицы, т. е. А, равно числу строк второй матрицы, т. е. В (но не наоборот!).
Произведением матрицы  на матрицу
на матрицу  , где
, где  называется такая матрица
называется такая матрица  , элементы которой вычисляются по формуле:
, элементы которой вычисляются по формуле:
 (1.21)
(1.21)
Обратите внимание на то, что в матрице С получилось столько строк, сколько их имела матрица А, и столько столбцов, сколько их было в матрице В.
Пример 4. Даны матрицы  ;
;  . Найти матрицу
. Найти матрицу 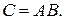
Решение.


Умножение матриц удовлетворяет следующим свойствам:
1)  4)
4) 
2) 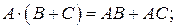 5)
5) 
3)  6)
6) 
если, конечно, написанные суммы и произведения матриц имеют смысл.
Матрицы 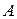 и
и  называются перестановочными, если
называются перестановочными, если  например, как видно из указанных выше свойств, матрицы
например, как видно из указанных выше свойств, матрицы 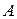 и
и  а также
а также 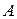 и
и  перестановочны.
перестановочны.
Замечание: в качестве упражнения докажите, что, например, матрицы
 и
и  не являются перестановочными.
не являются перестановочными.
Обозначение эквивалентных матриц 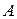 и
и 
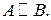
К элементарным преобразованиям матрицы относится любая из следующих операций:
1) перемена местами любых двух строк (столбцов);
2) умножение каждого элемента произвольной строки (столбца) на один и тот же отличный от нуля множитель;
3) вычеркивание строки (столбца), целиком состоящей из нулей;
4) прибавление к элементам произвольной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на произвольное число.
Путем элементарных преобразований любую ненулевую матрицу можно привести к матрице вида:
 . (1.25)
. (1.25)
2.СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
В качестве иллюстрации широты применения систем линейных алгебраических уравнений (СЛАУ) приведем несколько задач, приводящих к СЛАУ.
Начнем с примера задачи экономического содержания, которая, в конечном итоге, приводит к матричному уравнению. Математическая модель, позволяющая анализировать таблицы межотраслевого баланса в макроэкономике, разработана в 1936 г. В. Леонтьевым. Если рассматривать n отраслей промышленности, каждая из которых производит свою продукцию, то часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для конечного личного или общественного потребления.
Введем следующие обозначения:  – общий (валовой) объем продукции
– общий (валовой) объем продукции  -й отрасли
-й отрасли 
 – объем продукции
– объем продукции  -й отрасли, потребляемой
-й отрасли, потребляемой  -й отраслью в процессе производства
-й отраслью в процессе производства 
 – объем конечного продукта
– объем конечного продукта  -й отрасли для непроизводственного потребления.
-й отрасли для непроизводственного потребления.
Так как валовой объем продукции любой  -й отрасли равен суммарному объему продукции, потребляемой
-й отрасли равен суммарному объему продукции, потребляемой  отраслями, и конечного продукта, то
отраслями, и конечного продукта, то
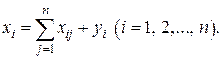 (2.1)
(2.1)
Введем коэффициенты прямых затрат 
 показывающие затраты продукции
показывающие затраты продукции  -й отрасли на производство единицы продукции
-й отрасли на производство единицы продукции  -й отрасли. В предположении, что в некотором промежутке времени коэффициенты
-й отрасли. В предположении, что в некотором промежутке времени коэффициенты 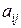 будут постоянными и зависящими от сложившейся технологии производства, это означает линейную зависимость материальных затрат от валового выпуска, т. е.
будут постоянными и зависящими от сложившейся технологии производства, это означает линейную зависимость материальных затрат от валового выпуска, т. е. 
 Таким образом, соотношения баланса (2.1) примут вид:
Таким образом, соотношения баланса (2.1) примут вид:
 (2.2)
(2.2)
Обозначим 
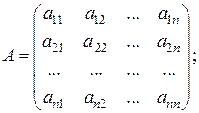
 где
где  – вектор валового выпуска;
– вектор валового выпуска;  – вектор конечного продукта;
– вектор конечного продукта; 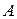 – матрица прямых затрат.
– матрица прямых затрат.
Тогда систему (2.1) можно записать в матричном виде: 
Рассмотрим теперь физические задачи, приводящие к СЛАУ.
Пусть мы имеем дело со схемой (рис. 2.1).
Рис. 2.1. Схема электрической цепи |
Слева направо течет общий известный ток  , который разветвляется в первом верхнем узле на
, который разветвляется в первом верхнем узле на  и
и 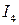 (токам присваиваются номера резисторов). Затем ток
(токам присваиваются номера резисторов). Затем ток  разветвляется во втором верхнем узле на
разветвляется во втором верхнем узле на  и
и  , а ток
, а ток  разветвляется в третьем верхнем узле на
разветвляется в третьем верхнем узле на  и
и  . В левом нижнем узле токи
. В левом нижнем узле токи 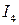 и
и  стекаются, и из узла вытекает ток
стекаются, и из узла вытекает ток  . В правом нижнем узле токи
. В правом нижнем узле токи  и
и  стекаются, и из этого узла вытекает ток
стекаются, и из этого узла вытекает ток  . В четвертом верхнем узле токи
. В четвертом верхнем узле токи  и
и  стекаются, и оттуда вытекает ток
стекаются, и оттуда вытекает ток  .Нужно найти все токи, кроме
.Нужно найти все токи, кроме  . Применение правил Кирхгофа к пяти узлам и трем контурам приводит к системе восьми линейных алгебраических уравнений для восьми токов:
. Применение правил Кирхгофа к пяти узлам и трем контурам приводит к системе восьми линейных алгебраических уравнений для восьми токов:
 (2.3)
(2.3)
Полученную систему уравнений (2.3) можно записать в матричном виде и решать, например, по формулам Крамера, которые рассматриваются ниже.
К СЛАУ приводит также задача определения начального положения  , начальной скорости
, начальной скорости 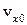 и ускорения
и ускорения  частицы при равнопеременном движении. Записываем соответствующие формулы для трех известных моментов времени –
частицы при равнопеременном движении. Записываем соответствующие формулы для трех известных моментов времени –  ,
, 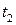 и
и  :
:
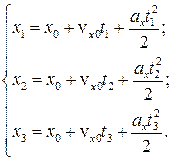 (2.4)
(2.4)
Полученную систему уравнений (2.4) также можно решить по формулам Крамера.
В заключение рассмотрим одну из задач линейного программирования: для изготовления двух видов продукции –  и
и  – используют четыре вида ресурсов –
– используют четыре вида ресурсов –  и
и  Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице.
Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице.
Данные к задаче
| Вид ресурса | Запас ресурса | Число единиц ресурсов, затрачиваемых на изготовление единицы продукции | |

| 
| ||

| |||

| |||

| – | ||

| – |
Прибыль, получаемая от единицы продукции  и
и  – 2 и 3 р. соответственно.
– 2 и 3 р. соответственно.
Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.
Если обозначить через  и
и  число единиц продукции
число единиц продукции  и
и  соот-ветственно, то экономико-математическую модель задачи можно записать в виде:
соот-ветственно, то экономико-математическую модель задачи можно записать в виде:

 (2.5)
(2.5)
При решении рассматриваемой задачи, например, симплексным методом в каждое из уравнений системы (2.5) вводят по одной из дополнительных неотрицательных переменных  в результате получают СЛАУ вида:
в результате получают СЛАУ вида:
 (2.6)
(2.6)
Дальнейшая процедура решения задачи состоит в преобразовании специальным образом составленной симплексной таблицы (использующиеся здесь формулы элементарных преобразований аналогичны элементарным преобразованиям расширенной матрицы СЛАУ, применяемым в методе Гаусса решения СЛАУ, который будет описан ниже).
Дата публикования: 2014-10-19; Прочитано: 528 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!











