Задача о четырех красках

Разбиение плоскости на непересекающиеся области называется картой. Области карты называются соседними, если они имеют общую границу. Задача состоит в раскрашивании карты таким образом, чтобы никакие две области не были закрашены одним цветом. С конца XIX века известна гипотеза, что для этого достаточно четырех красок. В 1976 году Аппель и Хейкен опубликовали решение задачи о четырех красках, которая базировалось на переборе вариантов с помощью компьютера.

Суть опубликованного решения состоит в том, чтобы перебрать большое, но конечное число (около 2000) типов потенциальных контрпримеров к теореме о четырех красках и показать, что ни один случай контрпримером не является. Этот перебор был выполнен программой примерно за тысячу часов работы суперкомпьютера. Проверить «вручную» полученное решение невозможно – объем перебора выходит за рамки человеческих возможностей. Многие математики ставят вопрос: можно ли считать такое «программное доказательство» действительным доказательством? Ведь в программе могут быть ошибки… Методы формального доказательства правильности программ не применимы к программам такой сложности, как обсуждаемая. Тестирование не может гарантировать отсутствие ошибок. Таким образом, остается уповать на программистскую квалификацию авторов и верить, что они все сделали правильно.

1. ГРАФЫ. ОРГРАФЫ

Графы и орграфы. Основные понятия

Определение 1.1. Графом 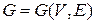называется совокупность двух множеств – непустого множества 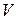(множества вершин) и множества 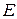двухэлементных подмножеств множества 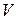. Множество 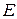называется множеством ребер.

Вершины и 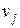множества 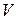называются соединенными ребром 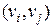или инцидентными к ребру 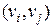, если . Если 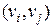– ребро, тогда вершины и 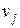называются концами ребра 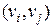. Ребро 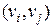называется также инцидентным к вершинам и 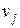. Две вершины называются смежными, если они инцидентны к одному ребру. Два ребра называются смежными, если они инцидентны к общей вершине.

Число вершин графа 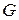обозначим 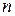, а число ребер − :

, .

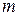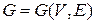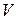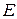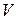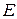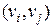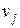Определение 1.2. Ориентированный граф или орграф – это такой граф, который состоит из множества вершин и множества упорядоченных пар элементов из . В этом случае элемент множества называется дугой. Если , то называется начальной вершиной дуги , а называется конечной вершиной.

Геометрическое представление графов следующее: вершина графа – точка в пространстве (на плоскости), ребро неориентированного графа – отрезок, дуга ориентированного графа – направленный отрезок.

Ребро, которое соединяет вершину саму с собой, называется петлей. Если в графе допускается наличие петель, то он называется графом с петлями или псевдографом. Если в графе допускается наличие более одного ребра между двумя вершинами, то он называется мультиграфом. Например, граф, построенный для решения задачи о кенигсбергских мостах, является мультиграфом. Если каждая вершина графа и (или) ребра помечена, то такой граф называется помеченным (или нагруженным). В качестве пометок обычно используются буквы или целые числа.

Если орграф содержит более чем одну дугу из одной вершины в другую, то называется ориентированным мультиграфом. Если каждая дуга помечена, то будем говорить, что это помеченный орграф.

Определение 1.3. Граф называется подграфом (или частью)графа 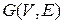, если , . Если , то называется остовным подграфом .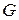

Аналогично, как и для графа, для орграфа вводится понятие ориентированный подграф.

Пример 1.1. Дан неориентированный граф.

,

Определение 1.4. Граф называется полным, если любые две его вершины соединены ребром. Полный граф с 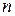вершинами обозначается через .

Определение 1.5. Граф 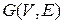называется двудольным, если 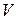можно представить как объединение непересекающихся множеств () так, что каждое ребро имеет вид 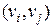, где и . Двудольный граф называется полным двудольным графом , если 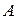содержит 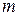вершин, 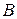содержит 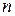вершин и для каждого , имеем .

Пример 1.2. Построить полный двудольный граф и полный граф .

,