Графический метод решения задач

При наличии в задаче линейного программирования двух переменных, а в системе ограничений — неравенств она может быть решена графическим методом.

В системе координат Х ₁ ОХ ₂ находят область допустимых решений, строят вектор 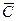и линию уровня. Перемещая линию уровня по направлению 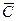для задач на максимум, находим наиболее удаленную от начала координат точку и ее коорди­наты.

В том случае, когда координаты этой точки нецелочислен­ные, в области допустимых решений строят целочисленную решетку и находят на ней такие целые числа, которые удовле­творяют системе ограничений и при которых значение целевой функции наиболее близко к экстремальному нецелочисленному решению. Координаты такой вершины и являются целочислен­ным решением.

Аналогично решается задача на минимум.