Транспортная параметрическая задача

Задача формулируется следующим образом: для всех зна­чений параметра δ ≤ λ ≤ φ, где δ, φ — произвольные дейст­вительные числа, найти такие значения x_ij (i = 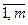; j = 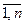), которые обращают в минимум функцию

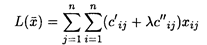
при ограничениях:

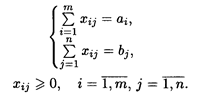
Пользуясь методом потенциалов, решаем задачу при λ = δ до получения оптимального решения. Признаком оптимально­сти является условие: u_i + v_j — [ c'_ij + λ с"_ij) ≤ 0 для незанятых клеток

и u_i + v_j = с' _ij + λ с''_ij для занятых клеток,

где u_i, v_j — потенциалы строк, столбцов распределительной таблицы.

Условие совместимости транспортной задачи запишется в виде

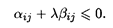
Значения α_ij и β_ij определяются из условия

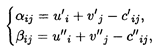
где u'_i, v'_i, u"_j, v"_j определяются из систем уравнений

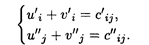
Значения λ находятся в пределах λ₁ ≤ λ ≤ λ₂:

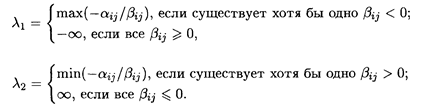
Алгоритм решения.

1) Задачу решаем при конкретном значении параметра λ = δ до получения оптимального решения.

2) Определяем α_ij и β_ij.

3) Вычисляем значения параметра λ.

4) Если λ < φ, производим перераспределение поставок и получаем новое оптимальное решение. Если λ = φ, то процесс решения окончен.