 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Определение диапазона оптимального решения выпуска продукции при изменении условий реализации
|
|
Рассмотрим следующую задачу.
Предприятие должно выпустить два вида продукции А и В, для изготовления которых используются три вида сырья. Нормы расхода сырья каждого вида на производство единицы данного вида приведены в табл 25.1. В ней указаны такие запасы сырья каждого вида, которые могут быть использованы на производство единицы продукции данного вида. Известно, что цена единицы продукции может изменяться для изделия А от 2 до 12 усл. ед., а для изделия В — от 13 до 3 усл. ед., причем эти изменения определяются выражениями 2 + λ и 13 — λ, где 0 ≤ λ ≤ 10.
Для каждого из возможных значений цены единицы продукции данного вида найти такой план их производства, при котором общая стоимость продукции является максимальной.

Решение. Обозначим через х 1 количество единиц продукции А, через x 2 — количество единиц продукции В. Математическая модель задачи имеет вид
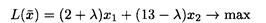
при ограничениях:
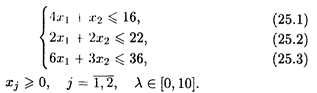
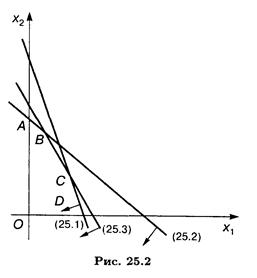
Область допустимых решений — многоугольник OABCD (рис. 25.2). Полагая λ = 0, L(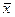 ) = 2 x 1 + 13 х 2 строим
) = 2 x 1 + 13 х 2 строим 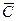 (2, 13). Перемещая линию уровня по направлению
(2, 13). Перемещая линию уровня по направлению 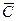 , находим, что в точке А (0, 11) задача имеет оптимальное решение. Таким образом, при λ = 0
, находим, что в точке А (0, 11) задача имеет оптимальное решение. Таким образом, при λ = 0 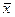 1опт(0, 11), L(
1опт(0, 11), L( 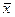 1 ) max = 143.
1 ) max = 143.
Если уравнение прямой имеет вид
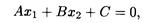
то угловой коэффициент равен k = - А/В.
Угловой коэффициент линии уровня, перпендикулярной 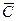 , при произвольном значении λ равен k = (2 + λ) / (13 – λ).
, при произвольном значении λ равен k = (2 + λ) / (13 – λ).
Найдем область оптимальности 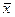 1опт :
1опт : 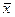 1опт будет оставаться оптимальным для всех λ, при которых соответствующая линия уровня находится внутри угла, образованного прямыми x 1 = 0 и (25.2). Угловой коэффициент прямой (25.2) k = - 2/2 = -1. По условию λ1 = 0, λ2 = (2 + λ) / (13 - λ) = -1, откуда λ2 = 11/2. Решение
1опт будет оставаться оптимальным для всех λ, при которых соответствующая линия уровня находится внутри угла, образованного прямыми x 1 = 0 и (25.2). Угловой коэффициент прямой (25.2) k = - 2/2 = -1. По условию λ1 = 0, λ2 = (2 + λ) / (13 - λ) = -1, откуда λ2 = 11/2. Решение 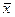 1опт остается оптимальным при λ
1опт остается оптимальным при λ 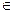 [0, 11/2].
[0, 11/2].
При λ = 11/2 линия уровня совпадает с прямой (25.2) и оптимальными будут все точки, лежащие на прямой (25.2), в том числе и точка В (1, 10), лежащая на пересечении прямых (25.2) и (25.3).
Оптимальное решение будет сохраняться до тех пор, пока при изменении λ линия уровня не совпадет с прямой (25.3), что будет соответствовать новому оптимальному решению 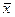 2опт. Найдем новый диапазон изменения λ: λ1 = 11/2, λ2 = (- 2 + λ) / (13 - λ) = -2, так как k 3 = -2. Откуда λ2 = 8.
2опт. Найдем новый диапазон изменения λ: λ1 = 11/2, λ2 = (- 2 + λ) / (13 - λ) = -2, так как k 3 = -2. Откуда λ2 = 8.
Получили при λ 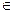 [11/2, 8]
[11/2, 8] 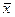 2опт = (1, 10), L(
2опт = (1, 10), L( 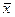 2 ) max =132 – 9λ.
2 ) max =132 – 9λ.
Аналогично определяем, что при λ 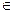 [8,10],
[8,10], 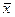 3опт = (2, 8), L (
3опт = (2, 8), L (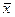 3)mах = 108 – 6λ.
3)mах = 108 – 6λ.
Таким образом, при λ = [0, 11/2] необходимо производить только 11 изделий В, при этом стоимость продукции будет максимальной и равной (143 – 11λ) усл. ед.; при λ 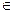 [11/2, 8] необходимо производить одно изделие А и 10 изделий В, при этом стоимость продукции является максимальной и равной (132 – 9λ) усл. ед.; при λ
[11/2, 8] необходимо производить одно изделие А и 10 изделий В, при этом стоимость продукции является максимальной и равной (132 – 9λ) усл. ед.; при λ 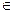 [8, 10] необходимо производить 2 изделия А и 8 изделий В, при этом стоимость продукции будет максимальной и равной (108 – 6λ) усл. ед.
[8, 10] необходимо производить 2 изделия А и 8 изделий В, при этом стоимость продукции будет максимальной и равной (108 – 6λ) усл. ед.
Найдем решение этой же задачи симплексным методом (табл. 25.2-25.4), для чего приведем задачу к каноническому виду:
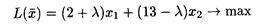
при ограничениях:
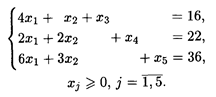
Получим λ1 = - 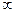 , так как все Δ ”j ≤ 0;
, так как все Δ ”j ≤ 0;
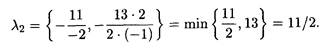
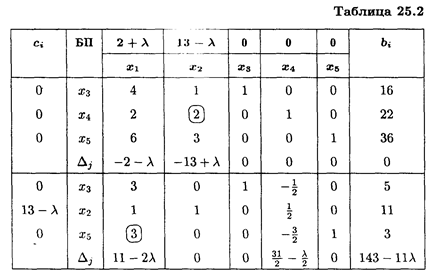

Таким образом, λ 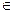 [0, 11/2],
[0, 11/2], 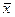 1опт = (0, 11, 5, 0, 3), L (
1опт = (0, 11, 5, 0, 3), L (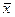 1)max = 143 – 11λ.
1)max = 143 – 11λ.
Получим

Таким образом, λ 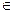 [11/2, 8],
[11/2, 8], 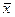 2опт = (1, 10, 2, 0, 0), L (
2опт = (1, 10, 2, 0, 0), L (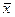 2)mах = 132 – 9λ.
2)mах = 132 – 9λ.
Получим
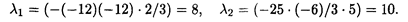
Таким образом, λ 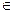 [8, 10],
[8, 10], 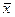 3опт = (2, 8, 0, 2, 0), L (
3опт = (2, 8, 0, 2, 0), L (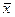 3)mах = 108 – 6λ.
3)mах = 108 – 6λ.
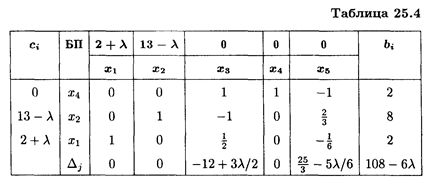
Получили следующие оптимальные решения в зависимости от диапазона изменения λ:
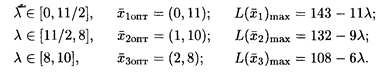
Дата публикования: 2014-10-18; Прочитано: 697 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
