 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Взаимно двойственные задачи линейного программирования и их свойства
|
|
Рассмотрим формально две задачи I и II линейного программирования, представленные в табл. 6.1, абстрагируясь от содержательной интерпретации параметров, входящих в их экономике-математические модели.
Эти две задачи обладают следующими свойствами:
1. В одной задаче ищут максимум линейной функции, в другой — минимум.
2. Коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений в другой.
3. Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида "  ", а в задаче минимизации все неравенства вида "
", а в задаче минимизации все неравенства вида "  ".
".
4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу:
для задачи I  ,
,
для задачи II  .
.
5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
6. Условия неотрицательности переменных имеются в обеих задачах.
Две задачи I и II линейного программирования, обладающие указанными свойствами, называются симметричными взаимно двойственными задачами. В дальнейшем для простоты будем называть их просто двойственными задачами.
Исходя из определения, можно предложить следующий алгоритм составления двойственной задачи.
1. Привести все неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задаче ищут максимум линейной функции, то все неравенства системы ограничений привести к виду "  ", а если минимум, то к виду "
", а если минимум, то к виду "  ". Для этого неравенства, в которых это требование не выполняется, умножить на –1.
". Для этого неравенства, в которых это требование не выполняется, умножить на –1.
2. Составить расширенную матрицу системы А 1, в которую включить матрицу коэффициентов при переменных А, столбец свободных членов системы ограничений и строку коэффициентов при переменных в линейной функции.
3. Найти матрицу  , транспонированную к матрице А 1.
, транспонированную к матрице А 1.
4. Сформулировать двойственную задачу на основании полученной матрицы  и условия неотрицательности переменных.
и условия неотрицательности переменных.
Пример 6.1. Составить задачу, двойственную следующей задаче:
 при ограничениях
при ограничениях

 .
.
Решение. 1. Так как исходная задача на максимизацию, то приведем все неравенства системы ограничений к виду "  ", для чего обе части первого и четвертого неравенства умножим на -1. Получим
", для чего обе части первого и четвертого неравенства умножим на -1. Получим

2. Составим расширенную матрицу системы
 .
.
3. Находим матрицу  , транспонированную к А
, транспонированную к А
 .
.
4. Формулируем двойственную задачу:
 при ограничениях
при ограничениях

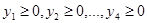 .
.
Дата публикования: 2014-10-18; Прочитано: 2910 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
