Глава 7. Транспортная задача

Экономико-математическая модель транспортной задачи

Важным частным случаем задачи линейного программирования является так называемая транспортная задача.

Пример 7.1. Построить экономико-математическую модель следующей задачи. Имеются три поставщика и четыре потребителя. Мощности поставщиков и потребителей, а также затраты на перевозку единицы груза для каждой пары поставщик-потребитель сведены в табл. 7.1 (таблицу поставок):

Таблица 7.1

Мощности потреби- Мощ- телей ности поставщиков

В левом верхнем углу произвольной (i, j) -и клетки (i — номер строки, j — номер столбца) стоит так называемый коэффициент затрат — затраты на перевозку единицы груза от i -го поставщика к j -му потребителю, например, в левом верхнем углу клетки (1,4) стоит число 3, следовательно, перевозка единицы груза от первого поставщика к четвертому потребителю обойдется в 3 (условных) денежных единицы и т.д.

Задача. Найти объемы перевозок для каждой пары поставщик-потребитель так, чтобы:

1) мощности всех поставщиков были реализованы;

2) опросы всех потребителей были удовлетворены;

3) суммарные затраты на перевозку были бы минимальны.

Решение. Построим экономикj-математическую модель данной задачи. Искомый объем перевозки от i -го поставщика к j -му потребителю обозначим через х_ij и назовем поставкой клетки (i,j). Например, x ₁₂— искомый объем перевозки от 1-го поставщика ко 2-му потребителю или поставка клетки (1, 2) и т.д. Заданные мощности поставщиков и потребителей накладывают ограничения на значения неизвестных х_ij. Так, например, объем груза, забираемого от первого поставщика, должен быть равен мощности этого поставщика — 60 единицам, т.е. (уравнение баланса по первой строке). Таким образом, чтобы мощность каждого из поставщиков была реализована, необходимо составить уравнения баланса для каждой строки таблицы поставок, т.е.

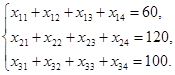(7.1)

Аналогично, чтобы спрос каждого из потребителей был удовлетворен, подобные уравнения баланса составляем для каждого столбца таблицы поставок:

(7.2)

Очевидно, что объем перевозимого груза не может быть отрицательным, поэтому следует дополнительно предположить, что .

Суммарные затраты F на перевозку выражаются через коэффициенты затрат и поставки следующим образом

(7.3)

Дадим математическую формулировку задачи (без обращения к ее содержательному экономическому смыслу)

Задача. На множестве неотрицательных решений системы ограничений (7.1), (7.2), найти такое решение при котором линейная функция (7.3) принимает минимальное значение.

Экономико-математическая модель транспортной задачи имеет следующие особенности:

- система ограничений есть система уравнений (т.е. транспортная задача задана в канонической форме);

- коэффициенты при переменных системы ограничении равны единице или нулю;

- каждая переменная входит в систему ограничений 2 раза: один раз в систему.(7.1) и один раз в систему (7.2).

Для математической формулировки транспортной задачи в общей постановке обозначим через с_ij коэффициенты затрат, M_i — мощности поставщиков, N_j — мощности потребителей, где i = 1, 2,..., m; j =1, 2,..., n, m — число поставщиков, п — число потребителей. Тогда система ограничений принимает вид

(7.4)

(7.5)

Система (7.4) включает в себя уравнение баланса по строкам, а система (7.5) — по столбцам таблицы поставок. Линейная функция в данном случае

. (7.6)

Тогда математическая формулировка транспортной задачи в общей постановке будет следующей: на множестве неотрицательных (допустимых) решений системы ограничений (7.4), (7.5) найти такое решение X = (х ₁₁, х ₁₂ ,..., x_ij..., х_тп), при котором значение линейной функции (7.6) минимально.

Произвольное допустимое решение X— (х ₁₁, х ₁₂ ,..., x_ij,..., х_тп) системы ограничений (7.4), (7.5) назовем распределением поставок. Такое решение задает заполнение таблицы поставок, поэтому в дальнейшем значение произвольной переменной x_ij и содержимое соответствующей клетки таблицы поставок будет отождествляться.

Транспортная задача, приведенная в примере 7.1, обладает важной особенностью: суммарная мощность поставщиков равна суммарной мощности потребителей, т.е.

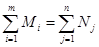. (7.7)

Такие транспортные задачи называются закрытыми (говорят также, что транспортная задача в этом случае имеет закрытую модель). В противном случае транспортная задача называется открытой (открытая модель транспортной задачи).

Рассмотрим закрытую транспортную задачу. Являясь задачей линейного программирования, транспортная задача может быть решена симплексным методом. Однако специфичная форма системы ограничений данной задачи позволяет существенно упростить обычный симплексный метод. Модификация симплексного метода применительно к транспортной задаче называется распределительным методом. По аналогии с общим случаем в нем решение также осуществляется по шагам, и каждому шагу соответствует разбиение переменных на основные (базисные) и неосновные (свободные).

Найдем, чему равно число r основных переменных транспортной задачи. Это число равно рангу системы линейных уравнений (максимальному числу линейно независимых уравнений в системе ограничений).

Теорема 7.1. Ранг r системы уравнений (7.4), (7.5) при условии (7.7) равен т + п -1.

Основное следствие теоремы 7.1 — число r основных (базисных) переменных закрытой транспортной задачи равно m + п - 1, где m - число поставщиков, n - число потребителей. Каждому разбиению переменных х_ij задачи на основные (базисные) и неосновные (свободные) соответствует базисное решение и, как следствие, заполнение таблицы поставок, которое также назовем базисным. Иными словами, распределение поставок называется базисным, если переменные, соответствующие заполненным клеткам, можно принять за основные переменные. Клетки, отвечающие базисным переменным, в дальнейшем будем называть базисными или заполненными, а клетки, отвечающие свободным переменным, - свободными или пустыми.

Подобно тому, как это было в симплексном методе, в распределительном методе решения транспортной задачи будем переходить от одного базисного распределения поставок к другому в сторону невозрастания целевой функции вплоть до оптимального решения. Для начала такого движения потребуется исходное базисное распределение поставок (так называемый опорный план).