Симплексные таблицы

Практические расчеты при решении реальных задач симплексным методом выполняются в настоящее время с помощью компьютеров. Однако, если расчеты осуществляются без ЭВМ, то удобно использовать так называемые симплексные таблицы. Далее мы рассмотрим алгоритм их составления, не углубляясь в его подробное обоснование. Для определенности считаем, что решается задача на отыскание максимума.

I. После введения добавочных переменных систему уравнений и линейную функцию записываем в виде, который называется расширенной системой:

Предполагаем, что все добавочные переменные имеют тот же знак, что и свободные члены; в противном случае — используем так называемый М-метод.

II. Исходную расширенную систему заносим в первую симплексную таблицу. Последняя строка таблицы, в которой записано уравнение для линейной функции цели, называется оценочной. В ней записываются коэффициенты функции цели с противоположным знаком: b_i = - c_i,. В левом столбце таблицы записываем основные переменные (базис), в первой строке таблицы — все переменные (отмечая при этом основные), второй столбец — свободные члены расширенной системы b ₁ b ₂,..., b_m. Последний столбец подготовлен для оценочных отношений, необходимых при расчете наибольшего возможно значения переменной. В рабочую часть таблицы (начиная с третьего столбца и второй строки) занесены коэффициенты а_ij при переменных из расширенной системы. Далее таблица преобразуется по определенным правилам. Проверяем выполнение критерия оптимальности при решении задачи на max — наличие в последней строке отрицательных коэффициентов . Если таких нет, то решение оптимально, достигнут max F = c ₀ (в левом нижнем углу таблицы); основные переменные принимают значения а_{i 0}(второй столбец), неосновные переменные равны 0, получаем оптимальное базисное решение.

IV. Если критерий оптимальности не выполнен, то наибольший по модулю отрицательный коэффициент b_i < 0 в последней строке определяет разрешающий столбец S.

Составляем оценочные ограничения каждой строки по следующим правилам:

1) , если имеют разные знаки; 2) , если и ;

3) , если ; 4) 0, если ;

5) , если имеют одинаковые знаки.

Определяем 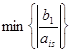. Если конечного минимума нет, то задача не имеет конечного оптимума (F _max = ). Если min конечен, то выбираем строку q, на которой он достигается (любую, если их несколько), и называем ее разрешающей строкой. На пересечении разрешающих строки и столбца находится разрешающий элемент a_qs.

V. Переходим к следующей таблице по правилам:

а) в левом столбце записываем новый базис — вместо основной переменной x_q переменную x_s;

б) в столбцах, соответствующих основным переменным, проставляем нули и единицы: 1 - против "своей" основной переменной, 0 - против "чужой" основной переменной, 0 – в последней строке для всех основных переменных;

в) новую строку с номером q получаем из старой делением на разрешающей элемент a_qs;

г) все остальные элементы вычисляем по правилу прямоугольника:

Рис. 5.4

Переходим к п. III алгоритма.

Пример 5.10. Решить задачу об использовании ресурсов, приведенную в § 1.2, с помощью симплексных таблиц (В примере 4.1 эта задача уже решена геометрически, а в примере 5.1 симплексным методом без использования таблиц).

Решение. Расширенная система задачи имеет вид (5.1):

Линейную функцию представим в виде: F - 2 х ₁ - 3 x ₂ = 0.

Заполняем первую табл. 5.1, в которой переменные х ₃, х ₄, х ₅ основные. Последняя строка заполняется коэффициентам линейной функции с противоположным знаком (см. п. II алгоритма).

Таблица 5.1

Базис	Свободный член	Переменные	Оценочное отношение
								18/3
F		-2	-3

В соответствии с п. III алгоритма проверяем критерий оптимальности. В последней строке имеются отрицательные коэффициенты.

Выбираем из них наибольший по модулю (-3); второй столбец разрешающий, переменная x ₂ перейдет в основные (этот столбец отмечен стрелкой). В соответствии с п. V находим оценочные отношения и х ₂ = min {18/3;16;5; } = 5. Третья строка является разрешающей (отмечена горизонтальной стрелкой). На пересечении разрешающих строки и столбца стоит разрешающий элемент a ₃₂= 1

Строим табл. 5.2 по правилам п. V:

а) в новом базисе основные переменные: х ₃, х ₄, х ₂, х ₆;

б) расставляем нули и единицы; например, в клетке, соответствующей основной переменной х ₃ по столбцу и строке, ставим 1, а в клетке, соответствующей основной переменной х ₂ по строке, а основной переменной х ₂ — по столбцу, ставим 0 и т.п. В последней строке против всех основных переменных ставим 0. Третья строка получается делением на разрешающий элемент а ₃₃ = 1. Остальные клетки заполняем по правилу прямоугольника. Например: и т.д. Получим вторую симплексную таблицу (табл. 5.2).

Таблица 5.2

Базис	Свободный член	Переменные	Оценочное отношение
						-3
						-1		11/2
F		-2

И на этот раз критерий оптимальности не выполнен, первый столбец разрешающий; х ₁ – переходит в основные, min{3; 11/2; ;7} = 3. Первая строка разрешающая, а ₁₁ – разрешающий элемент. Новая симплексная таблица примет вид (табл. 5.3):

Таблица 5.3

Базис	Свободный член	Переменные	Оценочное отношение
						-3
				-2				5/5
								5/1
				-3				12/9
F						-3

И на этот раз критерий оптимальности не выполнен, пятый столбец и вторая строка разрешающие, a ₂₅ = 5 — разрешающий элемент. Переходим к табл. 5.4.

Таблица 5.4

Базис	Свободный член	Переменные	Оценочное отношение
				-1/5	3/5
				-2/5	1/5
				2/5	-1/5
				3/5	-9/5
F				4/5	3/5

Критерий оптимальности выполнен, значит F _max = 24, оптимальное базисное решение (6;4;0;0;1;3) совпадает с ранее полученным (см. решение примера 5.1 симплексным методом).