Проблема идентификации. Необходимое и достаточное условие

Зная оценки приведенных коэффициентов модели, можно определить параметры структурной формы модели, но не всегда, а только если модель является точно идентифицируемой.

Модель считается точно идентифицированной, если все ее уравнения точно идентифицированы.

Модель считается не идентифицированной, если среди уравнений модели есть хотя бы одно не идентифицированное.

Модель считается сверх идентифицированной, если среди уравнений модели есть хотя бы одно сверхидентифицированное.

Уравнение называется точно идентифицированным, если оценки структурных параметров можно однозначно найти по коэффициентам приведенной формы модели.

Уравнение сверхидентифицировано, если для некоторых структурных параметров можно получить более одного численного значения.

Уравнение называется недентифицированным, если оценки его структурных параметров невозможно найти по коэффициентам приведенной формы модели.

Выполнение условия идентифицируемости проверяется для каждого уравнения системы по правилу: уравнение считается идентифицируемым, если число экзогенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.

Если обозначить число эндогенных переменных в j –oм уравнении системы через Н, а число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в данное уравнение через D, то условие идентифицируемости может быть записано в виде следующего счетного правила:

D+1 = H – уравнение идентифицируемо;

D+1 < H – уравнение неидентифицируемо;

D+1 > H – уравнение сверхидентифицируемо.

Рассмотренное счетное правило отражает необходимое, но недостаточное условие идентификации.

Достаточное условие идентификации - уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.

Ранг матрицы – размер наибольшей ее квадратной подматрицы, определитель которой не равен нулю.

Рассмотрим пример.

Пусть имеется система:

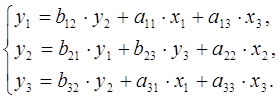(2.5)

Требуется проверить каждое уравнение структурной модели на идентификацию, применив необходимое и достаточное условие идентификации.

Решение:

В данной системе у₁, у₂ и у₃ - эндогенные переменные (Н = 3);

х₁, х₂ и х₃ – экзогенные переменные (D = 3).

Проверим каждое уравнение системы на необходимое и достаточное условия идентификации.

Первое уравнение.

Необходимое условие.

Уравнение содержит две эндогенных переменных: Н = 2 (у₁, у₂), отсутствует одна экзогенная переменная: D = 1 (х₂).

Выполняется необходимое равенство: 1 + 1 = 2, следовательно, уравнение точно идентифицируемо.

Достаточное условие.

В уравнении отсутствуют у₂ и х₂. Построим матрицу из коэффициентов при них в других уравнениях системы:

Уравнение	Отсутствующие переменные
у2	х2
Второе	-1	а22
Третье	b32

Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и первое уравнение точно идентифицируемо.

Второе уравнение.

Необходимое условие.

Уравнение содержит три эндогенных переменных: Н = 3 (у₁, у₂,, у₃,), отсутствуют две экзогенных переменных: D = 2 (х₁,х₃).

Выполняется необходимое равенство: 2 + 1 = 3, следовательно, уравнение точно идентифицируемо.

Достаточное условие.

В уравнении отсутствуют х₁ и х₃. Построим матрицу из коэффициентов при них в других уравнениях системы:

Уравнение	Отсутствующие переменные
х1	х3
Второе	а11	а13
Третье	а31	а33

Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и второе уравнение точно идентифицируемо.

Третье уравнение.

Необходимое условие.

Уравнение содержит две эндогенных переменных: Н = 2 (у₂,, у₃), отсутствует одна экзогенная переменная: D = 1 (х₂).

Выполняется необходимое равенство: 1 + 1 = 2, следовательно, уравнение точно идентифицируемо.

Достаточное условие.

В уравнении отсутствуют у₁ и х₂. Построим матрицу из коэффициентов при них в других уравнениях системы:

Уравнение	Отсутствующие переменные
у1	х2
Второе	-1
Третье	b21	а22

Определитель матрицы не равен 0, ранг матрицы равен 2; следовательно, выполняется достаточное условие идентификации, и третье уравнение точно идентифицируемо.

Следовательно, исследуемая система точно идентифицируема.