Примеры программирования с использованием средств пакета Matlab

Пример 4.5. Моделирование дискретного фильтра Калмана. Фильтр Калмана используется для построения оценок процессов при косвенных измерениях с ошибками. Подробно алгоритм описан в [14].

Текст m-сценария имеет вид:

%Дискретный фильтр Калмана

A=[0 1;0.05 0.9]; % матрица динамики

S=[0 1]; % матрица канала измерений

Q=[0.1 0;0 0.325]; V=0.09; % интенсивности

P=[0.03 0;0 0.05]; %начальная дисперсия

E=eye(2); %единичная матрица

x=[5 7.5]'; % начальные условия для объекта

xx=[0 0]'; % начальные условия для оценок

T=[]; X=[]; Y=[]; %объявление переменных

i=0;

while i<=20

T=[T i]; X=[X x]; Y=[Y xx];%формирование результата

x=A*x+Q*randn(2,1); % модель объекта

y=S*x+V*randn; %модель канала наблюдений

P1=A*P*A'+Q*Q'; %дисперсия прогноза

K=P1*S'*inv(S*P1*S'+V*V); %коэффициенты передачи фильтра

P=(E-K*S)*P1;% дисперсия оценки на очередном шаге

xx=A*xx+K*(y-S*A*xx);%вычисление оценки

i=i+1;

end;

subplot(2,1,1);

plot(T,X(1,:)',T,Y(1,:)');%графики 1-ой компоненты и ее оценки

grid;

subplot(2,1,2);

plot(T,X(2,:)',T,Y(2,:)');%графики 2-ой компоненты и ее оценки

grid;

Результаты вычислений приведены на рис 4.2; из них видно, что оценки процессов начинают удерживаться вблизи истинных значений практически, начиная с 1-го и 2-го такта.

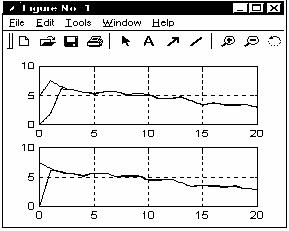
Рис. 4.1 - Результаты моделирования

Пример 4.6. Модальное управление. Смысл модального управления заключается в следующем. Необходимо для линейной динамической системы

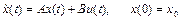, (4.1)

найти управление в виде 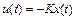, такое, чтобы матрица замкнутой динамики 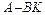имела заданные желаемые собственные числа. Эта задача решается средствами пакета Matlab. Выбор матрицы осуществляется с помощью m-функции пакета с именем place. Кроме того, программа вычисляет матрицу управляемости Калмана с помощью функции ctrb (m-файл, реализующий эту функцию приведен в примере 4.1).Ранг матрицы управляемости вычисляется с помощью функции rank (исходная система является управляемой, если ранг равен размерности исходного объекта). Решение дифференциального уравнения замкнутой системы

(4.2)

осуществляется с помощью функции ode45, реализующей метод Рунге-Кутта численного интегрирования дифференциальных уравнений (более подробно проблема численного решения дифференциальных уравнений описана в [3]). Ниже приведен текст m-сценария:

%Модальное управление

A=[0 1; 2 3];

B=[4 3]';

c=ctrb(A,B); %вычисление матрицы управляемости

rnk=rank(c);%вычисление ее ранга

disp('Ранг=')

disp(rnk);

disp('Если ранг равен 2 то система управляема')

r=[-0.3+i -0.3-i]';%желаемые собственные числа

K=place(A,B,r); %вычисление матрицы К

Phi=A-B*K;

rr=eig(Phi); %вычисление собственных чисел матрицы Phi

disp('Собств. числа=')

disp(rr) % вектор rr должен совпасть с r

x0=[1 0.1];

interval=[0 10];%временной интервал моделирования

[T,X]=ode45('model',interval,x0,[],Phi);

subplot(1,2,1)

plot(T,X)%графики переходных процессов

grid

subplot(1,2,2)

plot(X(:,1),X(:,2)) %фазовый портрет

grid

Используемая программой ode45 m-функция model, реализующая правую часть дифференциального уравнения (4.2), имеет вид:

function f=model(t,x,flag,L);

f=L*x;

Здесь t - независимая переменная; x - зависимая переменная; flag - строковая переменная, которая имеет вид возвращаемой информации; L - дополнительный параметр (их может быть несколько, разделяются запятыми), в m-сценарии это матрица Phi.

На рис 4.3 приведены переходные процессы в системе и фазовый портрет. Так как желаемые собственные числа имели отрицательные действительные части, то видим, что замкнутая система устойчива.

Рис. 4.2 - Переходные процессы и фазовый портрет

Пример 4.7. Оптимальное управление по квадратичному интегральному критерию. Предполагается, что модель объекта описывается уравнением (4.1). Требуется найти управление , минимизирующее квадратичный интегральный критерия вида:

,

где и - весовые матрицы. Оптимальное управление имеет вид:

,

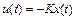где матрица вычислятся с помощью функции пакета Matlab lqr. Входные переменные этой функции являются матрицы , , и . Ниже приведен текст m-сценария:

%Оптимальное управление

global Phi

A=[0 1; 2 3]; B=[4 3]';

С =[1 0; 0 1]; D=1;

K=lqr(A,B,C,D)% вычисление оптимальной матрицы K

Phi=A-B*K;

eig(Phi) %вычисление собственных чисел

x0=[1 1];%начальные условия

tt=[0 3]; %временной интервал моделирования

[T,X]=ode45('fun',tt,x0);

plot(T,X)%графики переходных процессов

Используемый программой ode45 m-функция fun, реализующая правую часть дифференциального уравнения (4.2) имеет вид:

function f=fun(t,x);

global Phi

f=Phi*x;

return

Отметим, что в этом примере матрица Phi объявлена глобальной переменной. На рис 4.4 приведены переходные процессы.

Рис. 4.3 - Переходные процессы в оптимальной системе

Пример 4.8. М инимизации без ограничений. Рассмотрим задачу нахождения значений переменных и 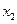, обеспечивающих решение задачи минимизации функции:

.

Нахождение решения производится в соответствии со следующими этапами.

1. Составление m-файла (с именем fun), реализующего вычисление значения целевой функции:

function f=fun(x)

f=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);

2. Составление программы с использованием подходящей функции пакета (в данном случае - функции fminunc):

x0=[-1,1];% начальные значения

options=optimset('LargeScale','off');

[x,fval,exitflag,output] = fminunc(‘fun’,x0,options)

Выполнение программы после нескольких шагов приведет к следующему результату:

Optimization terminated successfully

Current search direction is a descent direction, and magnitude of directional derivative in search direction less than 2*options TolFun

x =

0.5 -1.0000

Значение функции в точке х возвращается через fval:

fval=1.3030e-10,

exitflag > 0.

Значение exitflag=l (exitflag > 0) дает информацию, что найдена точка минимума (возможно, локального). Выходная структура (информация о результатах оптимизации) определяется идентификатором output:

число выполненных итераций (iterations): 7;

число вычислений функции (funcCount): 40;

шаг поиска (stepsize): 1;

степень оптимальности найденного решения (firstorderopt) - норма вектора-градиента в точке найденного решения:

8.1995е-004.

С помощью выбора переменных в опциях возможно в fminunc изменить характеристики оптимизационного алгоритма, например как x = fminunc(fun,x0,options). Структура options включает в себя значения точности окончания расчета и выбор алгоритма. Структура options может быть задана с помощью функции optimset: options = optimset('LargeScale','off'); В данном примере исключается принимаемый по умолчанию алгоритм для задачи большой размерности и был использован алгоритм средней размерности. Для задач большой размерности используется функция: options = optimset('LargeScale','on')

Пример 4.9. Минимизация с ограничениями. Пусть оптимизируемая функция будет таже, что и в примере 4.9. Ограничения имеют вид:

Определим функцию ограничений confun с ограничениями в форме неравенств:

function [c,ceq]=confun(x)

%огр. в форме неравенств

c=[1.5+x(1)*x(2)-x(1)-x(2);-x(1)*x(2)-10];

ceq=[];%в виде равенств ограничений нет

Основная программа:

x0=[-1,1];%начальные значения

options=optimset('LargeScale','off');

[x,fval]=fmincon('fun',x0,[],[],[],[],[],[],'confun',options)

Если минимизация осуществляется с дополнительным диапазоном в векторной форме:

,

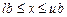то основная программа изменится и будет следующей:

x0=[-1,1];%начальные значения

lb=[0,0];%нижние границы

ub=[];%верхних ограничений нет

options=optimset('LargeScale','off');

[x,fval]=fmincon('fun',x0,[],[],[],[],lb,ub,'confun',options)

В последней строке четыре знака [],[],[],[] означают, что в задаче отсутствуют линейные ограничения в векторно-матричном форме (в виде равенств и неравенств) типа (4.3) и (4.5).

Пример 4.10. Метод наименьших квадратов ( МНК) для переопределенной системы

с ограничениями в векторно-матричной форме:

(4.3)

(4.4)

Пример программы для этой задачи с исходными данными имеет вид:

C=[0.951 0.762 0.615

0.231 0.45 0.79

0.61 0.185 0.922

0.48 0.82 0.738];

d=[0.578, 0.353,0.8131,0.0098]';

A=[0.203 0.272 0.747

0.198 0.199 0.445];

b=[0.5251,0.2026]';

lb=-0.1*ones(3,1);

ub=2*ones(3,1);

x=lsqlin(C,d,A,b,[],[],lb,ub)

Cимволы [] и [] в последней строке означают, что в задаче отсутствуют линейные ограничения в виде равенств вида

, (4.5)

где 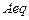- матрица, - вектор.

Пример 4.11. Определение минимакса. Постановка задачи формулируется следующим образом:

.

Программа для этой задачи в случае 5-ти мерной вектор-функции имеет вид:

x0=[0.1; 0.1];% начальные условия

[x, fval]=fminimax('myfun',x0)

Программа m-файла для вектор-функции цели:

function f=myfun(x)

f(1)=2*x(1)^2+x(2)^2-48*x(1)-40*x(2)+304;

f(2)=-x(1)^2-3*x(2)^2;

f(3)=x(1)+3*x(2)-18;

f(4)=-x(1)-x(2);

f(5)=x(1)+x(2)-8;

В задачах на минимакс могут учитываться как линейные так и нелинейные ограничения в виде равенств и неравенств.

Пример 4.12. Линейное программирование. Постановка задачи следующая:

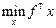(4.6)

при дополнительных ограничениях вида (4.3) – (4.5). В (4.6) - вектор-столбец, - вектор-столбец.

Конкретная программа при отсутствии линейных ограничений в виде равенств имеет вид:

f=[-5; -4; -6];

A=[1 -1 1;3 2 4;3 2 0];

b=[20; 42; 30];

lb=zeros(3,1);

ub=[];

x=linprog(f,A,b,[],[],lb,ub)

Пример 4.13. Квадратичное программирование. Постановка задачи следующая:

(4.7)

при дополнительных ограничениях вида (4.3) – (4.5). В (4.7) - матрица, - вектор-столбец, - вектор-столбец.

Ниже приведен пример программы.

H=[1 -1; -1 2];

f=[-2; -6];

A=[1 1; -1 2; 2 1];

b=[2; 2; 3];

x=quadprog(H,f,A,b)

В этом примере присутствуют только линейные ограничения в форме неравенств.

Отметим, что задачи максимизации функций сводятся к задачам минимизации тех же функций, но с противоположным знаком.

Пример 4.14. Оптимизация нормы матрицы при ограничениях в виде линейного матричного неравенства (типа неравенства Ляпунова). Необходимо найти матрицу как результат решения следующей задачи:

при ограничениях:

,

где - заданные матрицы. Пример программы решения подобной задачи имеет вид:

Q=[-1 -2; -2 -1];

P=[1 -1; -1 -3];

M=[10 0; 0 10];

X=basiclmi(M,P,Q,'Xmin')

Пример 4.15. Оптимизация следа матрицы при ограничениях в виде квадратичного матричного неравенства (типа неравенства Риккати). Необходимо найти матрицу как результат решения следующей оптимизационной задачи:

при ограничениях:

,

где - заданные матрицы. Пример программы решения данной оптимизационной задачи имеет вид:

A=[-1 -2 1; 3 2 1;1 -2 -1];

B=[ 1 0 1]’;

Q=[1 -1 0; -1 -3 -12; 0 -12 -36];

setlmis([])

X=lmivar(1,[3 1])

lmiterm([1 1 1 X],1,A,'s')

lmiterm([1 1 1 0],Q)

lmiterm([1 2 2 0],-1)

lmiterm([1 2 1 X],B',1)

LMIs=getlmis

C=mat2dec(LMIs,eye(3))

option=[1e-5,0,0,0,0]

[copt,xopt]=mincx(LMIs,C,option)

Xopt = dec2mat(LMIs,xopt,X)%фомирование результата

%в виде матрицы

Отметим, что пояснения смысла операторов, используемых в данной программе можно найти в комментариях, выполнив в командном окне команду help «имя оператора».

Пример 4.16. Построение аппроксимирующей нейронной сети (обобщенно-регрессионной). Ниже приведен пример программы с конкретными исходными данными..

in=[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15]%табличные значения

%аргумента

d=[0.2 3 2 5 6 7 8 5 4 3 2 1 1 2 2 ]%табличные значения

%функции

nf=newgrnn(in,d,0.4);%настройка нейронной сети

%по заданной обучающей выборке

%0.4 – допустимая ошибка

x=0:0.1:15 %входной массив

y=sim(nf,x);%опрос (моделирование) сети

plot(x,y,in,d,'*') %построение графика

На рис. 4.5 приведен график аппроксимирующей функции, построенной с помощью нейройной сети.

Рис. 4.4 - График аппроксимирующей функции

Пример 4.17. Линейная прогнозирующая нейронная сеть. Пример программы:

T=[14.0 14.7 14.7 15.1 15.2 15.3 15.8 16.0 17.2... %значения

20 20.2 23.1 23 22 20.9 22.1 22.2 24.1 28 27.9...%временного

26.2 24.5 22 20 22.2 23.3 22.6 21.4 22.8 22.2...%ряда

24.3 28.4 28.7 26.6 21.6 21.1 20.5 23.2 24.7 25.5];

Q=length(T);

time=1:Q;

M=max(T);

T=T./M; %масштабирование исходного временного ряда

P=zeros(5,Q);%5 - глубина памяти алгоритма прогноза

P(1,2:Q)=T(1,1:(Q-1));

P(2,3:Q)=T(1,1:(Q-2));

P(3,4:Q)=T(1,1:(Q-3));

P(4,5:Q)=T(1,1:(Q-4));

P(5,6:Q)=T(1,1:(Q-5));

net=newlind(P,T);%создание нейронной сети

%(проектирование нового линейного слоя)

a=sim(net,P);%опрос сети

e=T-a;%вычисление ошибки

subplot(2,1,1)

plot(time,M*a,time,M*T,'*')%построение графика

%прогнозируемых значений

subplot(2,1,2)

plot(time,M*e,time,0)%построение графика ошибок прогноза

На рис. 4.6 в верхнем окне приведен график значений прогноза и символом «*» обозначениы значения временного ряда, в нижнем окне приведен график ошибки прогноза

Рис. 4.5 - График значений прогноза и ошибок прогноза

Подробней вопросы построения нейронных сетей отражены в учебнике [1].

5. СИСТЕМА SIMULINK

В состав системы MATLAB 5.3 входит версия пакета Simulink 3.1. Этот пакет предназначен для математического моделирования линейных и нелинейных систем и устройств, которые представляются своей функциональной блок-схемой. Возможны различные варианты моделирования: во временной области, в частотной области, с событийным управлением, на основе спектральных преобразований Фурье, с использованием метода Монте-Карло и др.

Для построения функциональной блок-схемы моделируемых систем Simulink имеет обширную библиотеку блочных компонентов и удобный редактор блок-схем, использующий возможности графического интерфейса пользователя. По сути дела Simulink является средством визуального моделирования. Simulink использует технологию drag-and-drop (перетащи и оставь). Используя палитры комнетов блок-схем, пользователь с помощью мыши переносит нужные компоненты с палитр на свой рабочий стол пакета Simulink и соединяет линиями входы и выходы блоков. Блоки, включаемые в создаваемую модель, могут быть связаны друг с другом как по информации, так и по управлению. Тип связи зависит от типа блока и логики работы модели. Данные, которыми обмениваются блоки, могут быть скалярными величинами, векторами или матрицами произвольной размерности. Создаваемые модели могут иметь иерархическую структуру, то есть состоять из моделей более низкого уровня, причем число уровней иерархии практически не ограничено. В ходе моделирования пользователь может наблюдать за процессами, происходящими в системе. Для этого используются так называемые "смотровые окна", входящие в состав библиотеки Simulink. Интересующие пользователя характеристики могут быть представлены как в числовой, так и в графической форме, существует также возможность включения в состав модели средств анимации. Важным достоинством Simulink является то, что он представляет собой открытую систему. Состав библиотеки может быть пополнен пользователем за счет разработки новых блоков.

Запустить Simulink можно нажав соответствующую кнопку на панели меню командного окна:

В результате откроется окно:

Это окно представляет Simulink Library Browser, в котором мы можем отрыть библиотеку Simulink, а также самостоятельные пакеты в различных предметных областях, использующие блок-схемы Simulink.