Промежуточные вычислении 17 страница

Общая площадь склада = 25 футов²

Вручную производить вычисления в этой задаче утомительно, поэтому воспользу­емся шаблоном chllConstrainedEOQ.xls.

На рис. 11.6 показан рабочий лист этого шаблона с исходными данными для рас­сматриваемой задачи. Исходные данные содержат все необходимые параметры для каждого вида запаса (товара). Начальное значение Л (ячейка СЮ) обычно устанав­ливается равным нулю, шаг изменения Л задается в ячейке СИ. Это начальное зна­чение Л и шаг изменения определяют точность вычисленного значения Л и объем выполненных вычислений.

	в	с	D	E	F	G		H
			Constrained multi-item EOQ -	[sum(ay)<A
	Input data:
	Nbr. of items =
	Constraint RHS, A =		Enter 0 if sum(ay), 1 if sum(afy)
		Iteml	Item2	Item3
	Setup cost, К =
	Demand rate. D =
	Holding cost, h =	0.3	0.1	0.2
	Parameter, a =
	Initial X =
	X decrement =	0.1
	Output:
	Calculations:	Last tow gives the appioximate optimum
	Л	y1	У2	y3
	0 000000	11 55	20.00	24.49
	-0 100000	8 94	11.55	17.32
	-0.200000	7 56	8.94	14.14
	-0.300000	6.67	7.56	12.25
	-0.400000	6.03	6.67	10.95

Puc. 11.6. Решение в Excel задачи примера 11.2.3

Шаблон рассчитан на решение задач, содержащих не более 10 видов запаса. С по­мощью этого шаблона можно находить решение задач, где ограничение представ­лено в форме

11.2. Статические модели управления запасами

Такой тип ограничения может возникнуть в различных ситуациях, одна из них показана в упражнении 11.2.3.4. Для решения задач с таким типом ограничений следует ввести в ячейку G4 значение 1.

Данные в столбце М показывают, что значение Я* находится в интервале от -0,3 до -0,4. Шаблон позволяет получить значение Я с любой наперед заданной точностью. Для этого надо ввести в ячейку СЮ новое начальное значение -0,3 для Я и новое значение шага изменения, например 0,05. После ввода этих значений рабочий лист пересчитывается автоматически, в результате чего получаем новый (меньший) ин­тервал, содержащий значение Л. После нескольких подобных пересчетов я полу­чил значение Я* = -0,348, вычисленное с точностью 0,0005. Это значение Я* дает

у* = 6,34 единицы, у\ ~ 7,09 единицы, у\ ~ 11,57 единицы.

УПРАЖНЕНИЯ 11.2.3³

1. Приведенные ниже данные относятся к задаче управления запасами для пя­ти видов продукции.

Продукция / К, (долл.) D, (единиц в день) п, (долл.) а, (кв. футы)

1 20 22 0,35 1,0

2 25 34 0,15 0,8

3 30 14 0,28 1,1

4 28 21 0,30 0,5

5 35 26 0,42 1,2

Общая площадь склада = 25 футов²

Определите оптимальный объем заказа.

2. Решите задачу из примера 11.2.3, предполагая, что сумма средних запасов всех предметов должна быть меньше 25 единиц.

3. Решите предыдущее упражнение, предполагая, что единственным ограниче­нием является денежная сумма в 10 000 долл., которая может быть потраче­на на приобретение запасов продукции. Стоимость закупки единицы про­дукции вида 1, 2 и 3 равна соответственно 100, 50 и 100 долл.

4. Приведенные ниже данные относятся к задаче управления запасами для че­тырех видов продукции. Компания желает определить экономичный объем заказа для каждого из четырех видов продукции таким образом, чтобы сум­марное количество заказов в год (365 дней) было не более 150.

Продукция /	К, (долл.)	0, (единиц в день)	hi (долл.)
			0,1
			0,2
			0,2
			0,1

При выполнении этих упражнений рекомендуем использовать шаблон chllConstrainedEOQ.xls.

Глава 11. Детерминированные модели управления запасами

Запишите функцию Лагранжа и получите формулы, необходимые для реше­ния данной задачи.

5. На основе уравнения в частных производных задачи управления запасами этой главы покажите, что в качестве начального значения Я в процедуре по­иска оптимального значения этого параметра можно взять величину

д. _ h ггаКР

где

й=-^—, а=-&—, KD =—-.

п п п

Примените это начальное значение в задаче из примера 11.2.3.

11.3. ДИНАМИЧЕСКИЕ ЗАДАЧИ ЭКОНОМИЧНОГО РАЗМЕРА ЗАКАЗА

Рассматриваемые здесь модели отличаются от представленных в разделе 11.2. Во-первых, уровень запаса контролируется периодически на протяжении конечно­го числа одинаковых периодов. Во-вторых, объем спроса на протяжении периода хотя и является детерминированным, но в то же время он динамический, посколь­ку может периодически меняться.

Ситуация, в которой имеет место переменный детерминированный спрос, называет­ся планированием потребностей ресурсов. Подход к решению такой задачи рассмот­рим на примере. Предположим, что на протяжении следующего года квартальный спрос на модели Ml и М2 некоторой продукции равен 100 и 150 единиц соответственно. Поставки квартальных партий реализуются в конце каждого квартала. Срок выпол­нения заказа на модели Ml и М2 равен 2 месяца и 1 месяц соответственно. Для изго­товления каждой единицы модели Ml и М2 используется 2 единицы комплектую­щих деталей S. Срок изготовления комплектующих равен одному месяцу.

На рис. 11.7 схематически представлено календарное планирование производства моделей Ml и М2. Построение плана начинается с отображения в виде сплошных стрелок квартального спроса на две модели, который имеет место в конце 3-, 6-, 9-и 12-го месяцев. Затем при известных квартальных сроках пунктирные стрелки ука­зывают начало производства каждой партии продукции Ml и М2 в 1-й и 2-й месяцы.

Чтобы вовремя начать производство партий двух рассматриваемых моделей, по­ставка комплектующих S должна совпадать с началом производства Ml и М2, т.е. с пунктирными стрелками в планах их производства. Эта информация представле­на сплошными стрелками на S-схеме, где учитывается, что спрос на комплектую­щие S равен 2 единицам на каждую единицу продукции Ml и М2. Если учесть, что срок изготовления комплектующих равен одному месяцу, пунктирные стрелки на S-схеме определяют план производства комплектующих. Исходя из указанных двух планов, можно определить соответствующий суммарный спрос на S, как это показано в нижней части рис. 11.7. Результирующий переменный (но известный) спрос на комплектующие S представляет собой типичную ситуацию, когда приме­няются динамические модели экономичного размера заказа. При указанном пере­менном спросе на комплектующие S задача, по существу, сводится к определению

11.3. Динамические задачи экономичного размера заказа

объемов производства в начале каждого месяца для уменьшения затрат, связанных с производством и хранением продукции.

В этом разделе представлены две модели. В первой не учитывается стоимость размещения заказа, а вторая модель учитывает такие затраты. Эта "маленькая" деталь порождает соответствующие отличия в сложности моделей.

Модель 1

1 2 3 4 5 6 7 8 9 10 11 12 Ч—I—I—I—I—I—I—I—I—I—I—I

Модель 2

0 123456789 10 11 12 I—I—I—I—I—I—I—I—I—I—I—I—I

200 300 200 300 200 300 200 300 Комбинированные требования i i i i i i ■ i на комплектующие S для \—f—I—J—X—|—\—f—|—J—t—|—| изделий 1и2 0 123456789 10 11 12

Рис. 11.7. Календарное планирование производства двух моделей

УПРАЖНЕНИЕ 11.3.1

1. Определите суммарные потребности в комплектующих S в соответствии с рис. 11.7 в каждом из следующих случаев.

a) Поставка продукции Ml осуществляется каждый квартал.

b) Поставка продукции Ml осуществляется раз в три квартала.

11.3.1. Модель при отсутствии затрат на оформление заказа

В этой модели рассматривается задача календарного планирования производст­ва, рассчитанная на п равных периодов. Возможные объемы производства в каж­дый из периодов ограничены, однако они могут включать несколько уровней (например, два возможных объема производства могут определяться обычным ре­жимом работы и сверхурочными работами соответственно). На протяжении теку­щего периода могут производиться изделия для последующих периодов, но в этом случае должны учитываться затраты на их хранение.

Основные предположения модели состоят в следующем.

1. Отсутствие затрат на оформление заказа в любой период планирования.

2. Отсутствие (недопустимость) дефицита.

Глава 11. Детерминированные модели управления запасами

3. Стоимость производства единицы продукции в любой период либо является постоянной, либо имеет возрастающие предельные затраты (т.е. соответст­вующая функция затрат является выпуклой).

4. Стоимость хранения единицы продукции в каждый период является посто­янной величиной.

Предположение об отсутствии дефицита означает, что спрос на продукцию на протяжении текущего периода не может быть удовлетворен за счет ее производства в последующие периоды. Это предположение по крайней мере требует, чтобы сум­марные возможности производства за периоды 1, 2, i были равны суммарному спросу на продукцию за это же время.

На рис. 11.8 показано, когда производственные затраты на единицу продукции возрастают с увеличением уровня производства. Например, при двух возможных объемах производства, которые определяются обычным режимом работы и сверх­урочными работами, стоимость производства единицы продукции, производимой в сверхурочное время, выше, чем при обычном режиме работы.

Затраты

О Объем производства

Рис. 11.8. Выпуклая функция затрат

Рассматриваемую задачу п-этапного планирования можно сформулировать в виде транспортной задачи (см. главу 5) с kn пунктами производства и п потреби­телями, где k — количество возможных уровней производства на протяжении пе­риода (например, если на протяжении каждого периода используется регулярный и сверхурочный режимы работы, то k = 2). Производственные возможности каждо­го из kn пунктов производства определяют объемы поставок. Объемы потребления определяются объемом спроса для каждого периода. Себестоимость "перевозки" от пункта производства до пункта назначения определяется суммой затрат исполь­зуемого производственного процесса и стоимости хранения единицы продукции. Оптимальное решение такой транспортной задачи определит объемы производства продукции для каждого производственного уровня, которые минимизируют сум­марные затраты на производство и хранение.

Эту задачу можно решить без использования метода решения транспортных за­дач, представленного в главе 5. Обоснованность нового метода решения, показан­ного далее, следует из упомянутых предположений об отсутствии дефицита и вы­пуклости функции затрат на производство.

11.3. Динамические задачи экономичного размера заказа

Пример 11.3.1

Компания производит специальные вытяжки, которые используются в домашних каминах в период с декабря по март. В начале отопительного сезона спрос на эту продукцию низкий, в середине сезона он достигает своего пика и уменьшается к концу сезона. Учитывая популярность продукции, компания может использо­вать сверхурочные работы для удовлетворения спроса на свою продукцию. Сле­дующая таблица содержит данные о производственных мощностях компании и объемах спроса на протяжении четырех месяцев.

Возможности производства

Месяц Обычный режим работы (единицы) Сверхурочные (единицы) Спрос (единицы)

Стоимость производства единицы продукции равна 6 долл. в условиях обычного режима работы и 9 долл. при сверхурочных работах. Стоимость хранения единицы продукции на протяжении месяца равна 0,10 долл.

Чтобы гарантировать допустимое решение при отсутствии дефицита, требуется, чтобы суммарное предложение продукции (возможности производства) к началу каждого месяца по меньшей мере равнялось суммарному спросу. Об этом свиде­тельствует следующая таблица.

Месяц	Суммарное предложение	Суммарный спрос
	90 + 50 = 140
	140 + 100 + 60 = 300	100 + 190 = 290
	300 + 120 + 80 = 500	290 + 210 = 500
	500 + 110 + 70 = 680	500 + 160 = 660

В табл. 11.1 содержатся данные, относящиеся к рассматриваемой задаче, и ее ре­шение. Здесь R_t и О, соответствуют уровням производства в обычном и сверхуроч­ном режиме работы на протяжении периода i, i = l, 2, 3,4. Так как суммарное предложение в четвертом периоде превышает суммарный спрос, то введен искусст­венный пункт потребления (избыток), чтобы сбалансировать модель (это показано в табл. 11.1). Все "транспортные" маршруты из предыдущего в текущий период за­блокированы, так как дефицит отсутствует.

Себестоимости "перевозок" продукции вычисляются в виде суммы затрат на про­изводство и хранение. Например, соответствующая себестоимость от Я, до первого периода равна лишь стоимости изготовления в 6 долл., себестоимость от О, до чет­вертого периода — стоимости изготовления плюс стоимость хранения от первого периода до четвертого, т.е. 9 + (0,1 + 0,1 + 0,1) = 9,30 долл. Наконец, себестоимость перевозки до искусственного пункта потребления (избыток) равна нулю.

Оптимальное решение получается в один проход, начиная с первого столбца в на­правлении к столбцу "Избыток". Для каждого перспективного столбца спрос удов­летворяется с использованием самого дешевого маршрута⁴.

⁴ Доказательство оптимальности этой процедуры приведено в работе Johnson S.M. "Sequential Production Planning over Time at Minimum Cost", Management Science, Vol.3,1957, pp. 435-437.

490 Глава 11. Детерминированные модели управления запасами

Таблица 11.1

								Избыток
				6,1		6,2		6,3
я,
				9,1		9,2		9,3
о,										50->40->10
					6,1		6,2
Я2
					9,1		9,2
Ог
							6,1
Яз
							9,1
Оз
Я,
о4										70->20
	!	! !		! !		!

Начиная с первого столбца маршрут (Л,, 1) имеет самую дешевую себестоимость пе­ревозки, и мы назначаем перевозку максимально возможного объема, а именно min(90, 100) = 90 единиц, что оставляет 10 единиц неудовлетворенного спроса в первом столбце. Далее переходим к следующему по себестоимости маршруту (О,, 1) первого столбца и определяем перевозку min(50, 10) = 10 единиц, что теперь полностью удовлетворяет спрос для первого периода.

После удовлетворения спроса для первого периода мы переходим ко второму столбцу. Определение перевозок в этом столбце происходит следующим образом: 100 единиц по маршруту (R₂, 2), 60 единиц по маршруту (0₂, 2) и 30 единиц по маршруту (О,, 2). Этим маршрутам соответствуют себестоимости "перевозок" в 6, 9 и 9,10 долл. При этом маршрут (R,, 2), транспортные расходы на единицу продук­ции для которого равны 6,10 долл., не рассматривается, так как весь запас R, был израсходован для первого периода.

Продолжая аналогичным образом, мы удовлетворяем спрос для третьего, а затем и четвертого столбцов. Оптимальное решение, выделенное жирным шрифтом в табл. 11.1, интерпретируется следующим образом.

11.3. Динамические задачи экономичного размера заказа

Период

Производство

Период 1 (обычный режим работы) Период 1 (сверхурочный режим работы)

Период 2 (обычный режим работы) Период 2 (сверхурочный режим работы) Период 3 (обычный режим работы) Период 3 (сверхурочный режим работы) Период 4 (обычный режим работы) Период 4 (сверхурочный режим работы)

Изготовить 90 единиц продукции для первого периода

Изготовить 40 единиц продукции: 10 для периода 1, 30 для периода 2 и 10 для периода 3

Изготовить 100 единиц продукции для второго периода

Изготовить 60 единиц продукции для периода 2

Изготовить 120 единиц продукции для третьего периода

Изготовить 80 единиц продукции для периода 3

Изготовить 110 единиц продукции для четвертого периода

Изготовить 50 единиц продукции для периода 4; осталась неиспользованной производственная мощность на 20 единиц продукции

Соответствующие суммарные затраты при этом равны

90 х 6 + 10 х 9 + 30 х 9,10 + 100 х 6 + 60 х 9 + 10 х 9,20 + + 120x6 + 80x9 + 110x6 + 50x9 = 4685 долл.

УПРАЖНЕНИЯ 11.3.2

1. Решите задачу из примера 11.3.1, предполагая, что стоимости производст­ва и хранения единицы продукции имеют значения, приведенные в сле­дующей таблице.

Период /'	Стоимость единицы продукции при обычном режиме работы (долл.)	Стоимость единицы продукции при сверхурочном режиме (долл.)	Стоимость хранения единицы продукции до периода /' + 1
	5,00	7,50	0,10
	3,00	4,50	0,15
	4,00	6,00	0,12
	1,00	1,50	0,20

2. Изделие производится для удовлетворения заданного спроса на четырех вре­менных этапах в соответствии со следующими данными.

Удельные производственные затраты на этапах Диапазон объема производства _ (долл.) _

(единицы)
1-3
4-11
12-15
16-25
Затраты на хранение одного изделия до следующего этапа (долл.)	0,30	0,35	0,20	0,25
Суммарный спрос (единицы)

Г лава 11. Детерминированные модели управления запасами

a) Найдите оптимальное решение, определяющее количество изделий, кото­рые необходимо изготовить на каждом из четырех этапов.

b) Предположим, что на этапе 4 требуется 10 дополнительных изделий. На каких этапах следует их изготовить?

3. В течение последующих пяти этапов спрос на некоторое изделие можно удовлетворить при обычном режиме работы, сверхурочных работах и суб­подряде. Субподряды можно использовать лишь при недостатке возможно­стей сверхурочных работ. Данные о производственных мощностях и объемах спроса приведены в следующей таблице.

Производственные мощности (единицы)

Этап	Обычный режим работы	Сверхурочные работы	Субподряд	Спрос

Предполагается, что затраты на производство единицы продукции на всех этапах одинаковы и составляют 4, 6 и 7 долл. при обычном режиме работы, сверхурочных работах и субподряде соответственно. Затраты на хранение единицы продукции на каждом этапе равны 0,50 долл. Требуется найти оп­тимальное решение.

11.3.2. Модель с затратами на оформление заказа

В рассматриваемой модели предполагается, что дефицит не допускается и за­траты на оформление заказа учитываются всякий раз, когда начинается производ­ство новой партии продукции. Здесь будут рассмотрены два метода решения этой задачи: точный метод динамического программирования и эвристический.

Данная задача управления запасами схематически представлена на рис. 11.9. На этом рисунке использованы обозначения следующих величин, определенных для каждого этапа i, i = 1, 2.....п.

2, — количество заказанной продукции (объем заказа),

D, — потребность в продукции (спрос),

х, — объем запаса на начало этапа L

i+i

D.

*»+1

Рис. 11.9. Схема управления запасами с затратами на оформление заказа

Стоимостные элементы в рассматриваемой задаче определяются так: K_t — затраты на оформление заказа,

h_t — затраты на хранение единицы продукции, переходящей из этапа i в этап i +1.

11.3. Динамические задачи экономичного размера заказа

Соответствующая функция производственных затрат для этапа I задается формулой

где с[г) — функция предельных производственных затрат при заданном значении z_t.

Алгоритм динамического программирования с общей функцией стоимости. По­скольку дефицит не допускается, задача управления запасами сводится к вычисле­нию значений z_t, минимизирующих суммарные затраты, связанные с размещением заказов, закупкой и хранением продукции на протяжении п этапов. Затраты на хра­нение на £-м этапе для простоты предполагаются пропорциональными величине

которая представляет собой объем запаса, переходящего из этапа i в этап i + 1.

Для рекуррентного уравнения процедуры прямой прогонки состояние на этапе (пе­риоде) i определяется как объем запаса х_м на конец этапа, где, как следует из рис. 11.9,

Это неравенство означает, что в предельном случае запас x_j+l может удовлетворить спрос на всех последующих этапах.

Пусть /"|(х_1+]) — минимальные общие затраты на этапах 1,2, i при заданной величине запаса x_i+t на конец этапа i. Тогда рекуррентное уравнение алгоритма прямой прогонки будет записано следующим образом.

Требуется найти оптимальную стратегию в трехэтапной системе управления запа­сами, которая формулируется ниже. Начальный запас равен х₁ = 1 единице про­дукции. Предполагается, что предельные затраты на приобретение продукции со­ставляют 10 долл. за каждую единицу для первых трех единиц и 20 долл. — за каждую дополнительную единицу.

Период/ Спрос, D; (единицы) Затраты на оформление заказа, К,(долл.) Затраты на хранение, Л, (долл.) 13 3 1

2 2 7 3

3 4 6 2

Функция производственных затрат для периода i равна C_t(z) = K_l + c_t(z) для z_t > 0, где

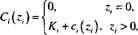
= ^Х, + ², ~ А

0 <*,₊₁<Д₊₁ +...+£>„.

Пример 11.3.2

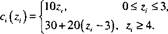
494 Глава 11. Детерминированные модели управления запасами

Этап 1. D, = 3, 0 < я₂ < 2 + 4 = 6.

Ci(zi) + Л1*₂ Оптимальное

Хг	h\x2	z, =2							решение
C,(z,) = 23
									23 2
									34 3
									55 4
									76 5
									97 6
									118 7
									139 8

Так как я, = 1, минимальное значение z, равно D, - х_г = 3 - 1 = 2.