Потенциальная энергия упруго деформированного стержня равна 2 страница

6. Вязкость

Идеальная жидкость, т.е. жидкость без внутреннего трения – абстракция. Всем реальным жидкостям и газам в большей или меньшей степени присуще внутреннее трение, называемое также вязкостью. Вязкость проявляется, в частности, в том, что возникшее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается. Примером может служить движение жидкости в стакане после того, как её перестают размешивать ложечкой.

Для выяснения закономерностей, которым обладают силы внутреннего трения, рассмотрим следующий опыт. В жидкость погружены две параллельные друг другу пластины (рис. 9.5), линейные размеры которых значительно превышают расстояние между ними. Нижняя пластина удерживается на месте, верхняя приводится в движение с некоторой скоростью 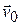. Опыт показывает, что для перемещения верхней пластины с этой скоростью необходимо действовать на неё с некоторой определенной постоянной по модулю силой 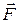. Так как пластина не получает ускорения, то действие этой силы должно уравновешиваться равной ей по модулю противоположно направленной силой, которая и есть сила внутреннего трения, действующая на пластину при её движении в жидкости. Обозначим эту силу через .

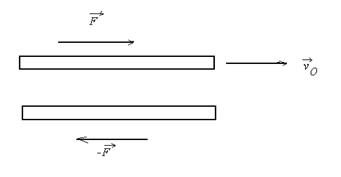
Рис. 9.5.

Опыт показывает, что

, (9.10)

где – площадь пластин, – расстояние между ними, 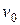– скорость пластины, а 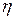– коэффициент пропорциональности, зависящий от природы и состояния (например, от температуры) жидкости и называемый коэффициентом внутреннего трения или просто вязкостью жидкости (газа).

Нижняя пластина при движении верхней также подвергается действию силы 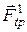, равной по модулю 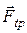. Для того чтобы нижняя пластина оставалась неподвижной, силу 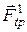необходимо уравновесить с помощью силы .

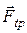Таким образом, при движении двух погруженных в жидкость пластин относительно друг друга между ними возникает взаимодействие, характеризуемое силой (9.10). Воздействие пластин друг на друга осуществляется через жидкость, заключенную между пластинами, передаваясь от одного слоя жидкости к другому. Если исследовать скорость частиц жидкости в разных слоях, то оказывается, что она изменяется в направлении z, перпендикулярном к пластинам, и по линейному закону

(9.11)

Частицы жидкости, непосредственно соприкасающиеся с пластинами, как бы прилипают к ним и имеют такую же скорость, как и сами пластины. Согласно формуле (9.11)

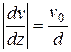(9.12)

Тогда модуль силы внутреннего трения определится по формуле

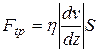(9.13)

Величина показывает, как быстро изменяется скорость в направлении оси z и представляет собой модуль градиента скорости.

Единицей вязкости в СИ служит паскаль-секунда (Па·с). Это такая вязкость, при которой градиент скорости с модулем равным 1 м/с на 1 м приводит к возникновению силы внутреннего трения в 1 Н на 1 м² поверхности касания слоев.

В СГС-системе единицей вязкости является пуаз (Пз), причем 1 Па·с = 10 Пз.

Коэффициент вязкости зависит от температуры. У жидкостей коэффициент вязкости уменьшается с повышением температуры. У газов, напротив, коэффициент вязкости с температурой растет.

7. Ламинарное и турбулентное течения

Наблюдаются два вида течения жидкости (или газа): ламинарное и турбулентное. Ламинарное течение – это течение, при котором жидкость как бы разделяется на слои, которые скользят относительно друг друга не перемешиваясь. Ламинарное течение стационарно.

При увеличении скорости или поперечных размеров потока характер течения существенным образом изменяется. Возникает энергичное перемешивание жидкости. Такое течение называется турбулентным. При этом течение нестационарно, так как скорость частиц изменяется беспорядочным образом. Если в турбулентный поток ввести окрашенную струйку, то уже на небольшом расстоянии от места введения окрашенная жидкость равномерно распределяется по всему сечению потока.

Английский физик Рейнольдс установил, что характер течения зависит от значения безразмерной величины

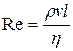, (9.14)

где ρ – плотность жидкости (или газа), v – средняя скорость потока (по сечению трубы), η – коэффициент вязкости жидкости, l – характерный для поперечного сечения размер, например, сторона квадрата при квадратном сечении, радиус или диаметр при круглом сечении и т.д.

Величина (9.14) называется числом Рейнольдса. При малых значениях числа Рейнольдса наблюдается ламинарное течение. Начиная с некоторого определенного значения 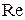, называемого критическим, течение приобретает турбулентный характер. Практически критическое число Рейнольдса равно примерно 1000.

В число Рейнольдса входят две величины, зависящие от свойств жидкости: плотность и коэффициент вязкости. Отношение 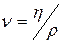называется кинематической вязкостью. В отличие от неё величина 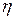называется динамической вязкостью. Используя кинематическую вязкость, числу Рейнольдса можно придать следующий вид: .

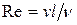Число Рейнольдса служит важным параметром моделирования процессов, в частности при обтекании тел.

8. Течение вязкой жидкости в круглой трубе. Формула Пуазейля

Пусть по горизонтальной трубе радиуса 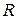течет стационарный поток жидкости. Рассмотрим отрезок этой трубы длиной (рис. 9.6).

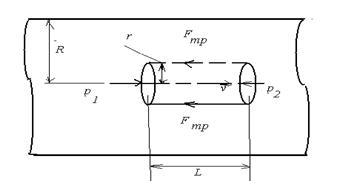
Рис. 9.6.

Частицы жидкости движутся вдоль трубы с разной скоростью: у самой стенки они прилипают к ней и имеют скорость равной нулю. По мере удаления от стенок скорость увеличивается и достигает максимального значения на оси трубы. Таким образом, величина скорости частиц жидкости является функцией 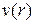расстояния 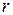от оси трубы.

Для доказательства этого утверждения выделим воображаемый цилиндрический объем жидкости радиуса 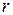. Жидкость, находящаяся внутри цилиндра, подвергается действию сил со стороны окружающей жидкости. Обозначим через – давление жидкости у основания 1, 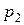– давление жидкости у основания 2, 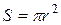– площадь оснований. Так как движение частиц жидкости происходит вдоль трубы, рассмотрим силы, действующие лишь в этом направлении. На основание цилиндра действуют силы давления, величины которых 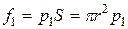и .

На боковую поверхность действует сила внутреннего трения 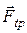. Так как скорость жидкости внутри цилиндра больше, чем вне его, то сила 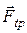направлена в сторону, противоположную движению жидкости. Величина этой силы определяется по формуле .

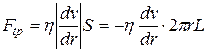Здесь знак минус поставлен потому, что скорость убывает с расстоянием от оси трубы, следовательно, отрицательна и

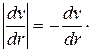
При стационарном течении в трубе постоянного сечения скорости всех частиц жидкости остаются неизменными. Следовательно, должна быть равна нулю сумма проекций на направление оси трубы всех сил, действующих на цилиндр, т.е. .

Здесь за положительное направление принято направление движения жидкости. Подставив сюда выражения для 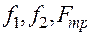, найдем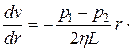

Разделив переменные, получим уравнение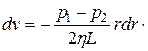

Интегрирование дает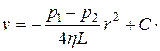

Постоянную интегрирования С можно найти из условия, что на стенке трубы, т.е. при скорость частиц должна обращаться в нуль. Это дает

Окончательно имеем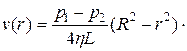

Отсюда видно, что при ламинарном течении скорость в зависимости от r меняется по параболическому закону и достигает максимума на оси трубы при 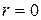(как это и предполагалось ранее) (рис. 9.7).

Рис.9.7. Профиль скоростей при ламинарном течении жидкости в круглой трубе

При турбулентном течении остается постоянной средняя скорость в каждой точке сечения трубы (рис.9.8). Вблизи стенок трубы скорость изменяется гораздо сильнее, чем при ламинарном течении, а в остальной части сечения скорость изменяется меньше.

Рис.9.8. Профиль скоростей при турбулентном течении жидкости в круглой трубе

Полагая течение ламинарным, вычислим поток жидкости Q, т.е. количество жидкости m, протекающей через поперечное сечение трубы за единицу времени t: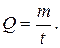

Разобьем поперечное сечение трубы на кольца ширины dr (рис. 9.9).

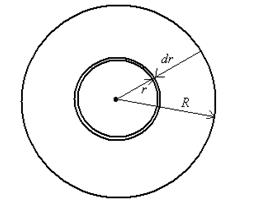
Рис.9.9.

Через кольцо радиуса r пройдет за секунду объем жидкости, равный произведению плотности жидкости 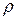на площадь кольца 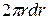и на скорость течения в точках, находящихся на расстоянии r от оси трубы.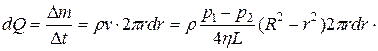

Полный расход Q через все поперечное сечение трубы определяется суммой расходов через все кольцевые площадки, на которые может быть разбито поперечное сечение. Он равен интегралу от dQ в пределах от r=0 до r=R:

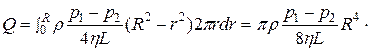
Эта формула называется формулой Пуазейля.

Из этой формулы следует, что поток жидкости сильно зависит от радиуса трубы. Кроме того, Q пропорционален отношению , т.е. перепаду давления на единице длины трубы, а также обратно пропорционален вязкости жидкости .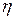

Формула Пуазейля используется для экспериментального определения вязкости жидкостей и газов. Для этого жидкость или газ пропускают через трубку известного радиуса, измеряют перепад давления и поток Q. Затем на основании известных данных вычисляют .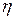

9. Движение тел в жидкостях и газах. Закон Стокса

При движении тела в жидкости или газе на него действуют две силы: сила 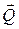, направленная в сторону, противоположную движению тела, а вторая 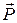, перпендикулярная к этому направлению. Составляющие 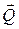и 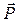называются соответственно лобовым сопротивлением и подъемной силой.

Ясно, что идеальная жидкость не оказывает движению тела никакого сопротивления.

Можно показать, что в несжимаемой идеальной жидкости равномерное движение тела произвольной формы должно было бы происходить без лобового сопротивления. Этот результат называется парадоксом Даламбера.

Учет вязкости жидкости существенно меняет картину взаимодействия тела с потоком. В этом случае очень тонкий слой жидкости прилипает к поверхности тела и движется с ним как одно целое, увлекая за собой из-за трения последующие слои. По мере удаления от поверхности тела скорость слоев становится все меньше и, наконец, на некотором расстоянии от поверхности оказывается практически не возмущенной движением тела. Таким образом, тело оказывается окруженным слоем жидкости, в котором имеется градиент скорости. Этот слой называется пограничным. В нем действуют силы трения, которые и приводят к возникновению лобового сопротивления.

Наличие пограничного слоя существенно меняет характер обтекания тела жидкостью. Полное обтекание тела становится невозможным. Действие сил трения в поверхностном слое приводит к тому, что поток отрывается от поверхности тела, в результате чего позади тела возникают вихри. Вихри уносятся потоком и постепенно затухают вследствие трения. При этом энергия вихрей расходуется на нагревание жидкости. Давление в образующейся за телом вихревой области оказывается пониженным. Поэтому результирующая сил давления будет отлична от нуля. Это давление в свою очередь обуславливает лобовое сопротивление.

Таким образом, лобовое сопротивление складывается из сопротивления трения и сопротивления давления.

При малых числах Рейнольдса сопротивление среды обусловлено практически только силами трения. Стокс установил, что сила сопротивления в этом случае пропорциональна коэффициенту динамической вязкости 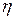, скорости движения тела относительно жидкости и характерному размеру тела 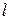: ~ . Коэффициент пропорциональности зависит от формы тела. Чаще всего его определяют экспериментальным путем. Вычисления Стокса показали, что для шара коэффициент пропорциональности оказывается равным 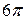. Тогда сила лобового сопротивления для шара радиуса при 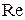<<1 выражается формулой .

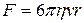Эта формула известна под названием закона Стокса. Она может быть использована для нахождения вязкости.

При больших числах Рейнольдса влияние вязкости существенно лишь в тонком пограничном слое жидкости, прилегающем к поверхности тела. Как уже было отмечено, это влияние приводит к образованию вихрей сзади тела. Перед телом частицы жидкости в набегающем потоке практически останавливаются, движутся они только за телом. Поэтому, согласно уравнению Бернулли, создается разность давлений, действующих на переднюю 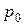и заднюю р поверхности тела. Она равна .

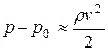Таким образом, сила лобового сопротивления определяется силой сопротивления давления: .

Для тел произвольной формы сила лобового сопротивления представляет вид , где – наибольшая площадь поперечного сечения тела, С – коэффициент лобового сопротивления.

Величина С зависит от формы тела и числа Рейнольдса. Величина С уменьшается, если уменьшить площадь поперечного сечения тела в том месте, где происходит отрыв потока. Обтекаемые тела испытывают значительно меньшее сопротивление, чем тела с тупой задней частью, так как у первых отрыв потока происходит в задней узкой части тела.

10. Истечение жидкости из отверстия

Рассмотрим истечение идеальной несжимаемой жидкости из небольшого отверстия в широком открытом сосуде (рис. 9.10).

Рис. 9.10.

В жидкости мысленно выделим трубку тока, сечениями которой являются открытая поверхность жидкости 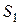и сечение струи при выходе из отверстия (если не принять специальных мер, то сечение струи будет меньше отверстия). Для всех точек каждого из этих сечений скорость жидкости и высоту h над некоторым исходным уровнем можно считать одинаковыми. Поэтому к данным сечениям можно применить теорему Бернулли. Давления и 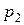в обоих сечениях одинаковы и равны атмосферному. Скоростью перемещения открытой поверхности жидкости ввиду ее малости можно пренебречь. Обозначим через v –скорость жидкости в сечении (скорость истечения из отверстия). Поэтому уравнение Бернулли в данном случае упрощается следующим образом: .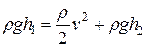

Сократив на плотность жидкости 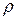, можно написать, что

(9.15)

где 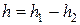– высота открытой поверхности над отверстием.

Формула (9.15) называется формулой Торричелли. Из нее следует, что скорость истечения жидкости из отверстия, находящегося на глубине под открытой поверхностью жидкости, совпадет со скоростью, которую приобретает любое тело, падая с высоты (в случае, если сопротивлением воздуха можно пренебречь). Этот результат получен в предположении, что жидкость идеальна. Для реальных жидкостей скорость истечения будет меньше, причем тем сильнее отличатся от значения, определяемого формулой Торричелли, чем больше внутреннее трение в жидкости. Например, глицерин будет вытекать из сосуда медленнее, чем вода.

Контрольные вопросы

1. Что такое давление в жидкости? Давление – величина векторная или скалярная? Какова единица измерения давления в СИ?

2. Сформулируйте и поясните законы Паскаля и Архимеда?

3. Что называют линией тока? трубкой тока?

4. Что характерно для установившегося течения жидкости?

5. Каков физический смысл и как вывести уравнение неразрывности для несжимаемой жидкости?

6. Какой закон выражает уравнение Бернулли для идеальной несжимаемой жидкости? Выведите это уравнение.

7. Что такое градиент скорости?

8. Каков физический смысл коэффициента динамической вязкости?

9. Какое течение называют ламинарным? Турбулентным? Что характеризует число Рейнольдса?

10. Поясните практическое применение методов Стокса и Пуазейля?

11. Каковы причины возникновения лобового сопротивления тела, движущегося в жидкости? Может ли оно быть равным нулю?

12. Как объяснить возникновение подъемной силы?

13. Найти выражение потенциальной энергии тела, погруженного в жидкость.

14. Найти зависимость выталкивающей силы Архимеда от глубины погружения.

15. Сосуд с жидкостью падает с ускорением . Как меняется давление с изменением глубины?

16. Может ли быть одинаковым давление в двух точках, лежащих на разных уровнях в установленной наклонно сужающейся трубке, по которой течет идеальная жидкость?

17. Почему струя жидкости, вытекающая из отверстия, по мере удаления от отверстия все больше сжимается?

Лекция №10. Движение в неинерциальных системах отсчета

1. Неинерциальные системы отсчета

Системы отсчета, движущиеся относительно инерциальной системы с ускорением, называются неинерциальными. В неинерциальных системах законы Ньютона несправедливы. Эту несправедливость можно обнаружить на примере тела, покоящегося в некоторой инерциальной системе. В этом случае тело не испытывает действия сил . Однако в неинерциальной системе, движущейся по отношению к инерциальным системам с ускорением, тело будет иметь ускорение а, отличное от нуля. Поскольку , равенство не соблюдается.

Рассмотрим две системы отсчета (рис.10.1), из которых система К является инерциальной, а система К' движется относительно К с некоторым ускорением и, следовательно, неинерциальна.

Рис.10.1.

Движение частицы относительно системы К характеризуется радиус-вектором , а относительно системы К' – радиус-вектором 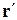, а вектор определяет положение начала координат системы К' относительно системы К.

Эти радиус-векторы связаны соотношением

Дифференцировав это соотношение дважды по времени, получим равенство

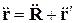(10.1)

Первая производная в (10.1) дает ускорение частицы а в системе К, вторая – ускорение начала О' системы К' относительно системы К.

С производной 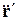дело обстоит сложнее: если система К' в дополнение к поступательному движению еще и вращается с угловой скоростью 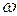, то эта производная, кроме ускорения а' частицы в системе К', содержит слагаемые, в которые входят множителями либо 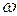, либо 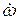. Это обусловлено тем, что 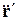в (10.1) представляет собой производную, вычисленную наблюдателем, находящимся в системе К. А а' есть вторая производная 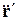, вычисленная наблюдателем, который вращается вместе с системой К'. Вектор 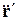ведет себя в обеих системах по-разному.

В случае, когда система К' движется относительно К поступательно (т.е. ), 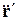= а' и соотношение (10.1) можно представить в виде

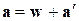(10.2)

2. Силы инерции

-121

Умножим равенство (10.2) на массу частицы m: .

Здесь произведение есть сила 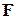, с которой действуют на частицу другие тела согласно второму закону Ньютона. В результате получим уравнение

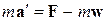(10.2)

Отсюда видно, что относительно системы К' частица ведет себя так, как если бы кроме «реальной» силы F на нее действовала дополнительная «фиктивная» сила 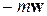. Эта сила называется силой инерции. Обозначим ее как . Фиктивность силы инерции надо понимать в том смысле, что не существует тел, воздействием которых была бы обусловлена эта сила. У нее нет «партнера», т.е. второй силы, предписываемой третьим законом Ньютона. Сила инерции обусловлена свойствами (неинерциальностью) той системы отсчета, в которой рассматриваются механические явления.