Построение обратной решетки

Рассмотрим элементарную ячейку гранецентрированной решетки. Выделим базисные атомы, соединим их векторами и на этих векторах, как на векторах трансляции, построим примитивную решетку для ГЦК структуры. Эта решетка представляет собой ромбоэдр (рис. 46).

;

;

;

Рис. 46. Ромбоэдр для ГЦК решетки

;

;

;

.

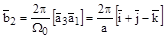Данный результат может быть интерпретирован следующим образом: направление вектора совпадает с направлением [ ], с направлением [ ], с направлением [ ].

На векторах , , 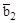в обратном пространстве построим элементарную ячейку. Нетрудно видеть, что симметрия полученной элементарной ячейки совпадает с симметрией объемно центрированного куба (рис. 47).

Если прямое пространство характеризуется симметрией объемно центрированного куба, обратное пространство будет представлено структурой гранецентрированного куба. Следовательно, если рассматривается движение электронов в периодическом поле структуры на основе ГЦК решетки, волновую функцию электрона мы будем рассчитывать в пространстве, симметрия которого совпадает с симметрией ОЦК.

Движение электронов в периодическом поле описывается при помощи волнового вектора

.

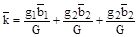Здесь G – достаточно большое число (нечетное).

Рис. 47. Ромбоэдр для ОЦК решетки

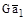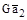Для того чтобы избежать трудностей, связанных для конечного кристалла с заданием граничных условий, разобьем бесконечный кристалл на одинаковые параллелепипеды с ребрами , , . Заменим граничные условия условиями цикличности Борна–Кармана, согласно которым все физические свойства и функции (волновая функция, волна колебаний атомов кристалла и т.д.) имеют одинаковое значение в точках и (i =1, 2, 3), т. е. периодически повторяются во всех параллелепипедах, на которые мы разбили бесконечный кристалл.

Применение условий цикличности позволяет рассматривать все явления и свойства кристалла в пределах одного выделенного в нем параллелепипеда (основной области) объемом , где – объем элементарной ячейки кристалла. Условиям цикличности Борна–Кармана в случае трехмерного кристалла нельзя придать столь наглядный смысл, как в случае одномерной цепочки равноотстоящих атомов. Однако можно показать, что в математическом отношении цикличности для трехмерного кристалла эквивалентны любым граничным условиям на поверхности основной области, не влияющим на объемные свойства кристалла

.

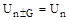Если волновой вектор 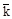заменить на 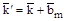, где то

,

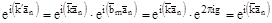где g – целое число.

Состояния, характеризующиеся волновыми векторами и 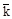, неразличимы.

Условия цикличности сводятся к требованию, чтобы волновое поле оставалось неизменным при смещении на любой из векторов , т. е.

, т. е. ;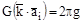

, откуда .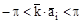

В этом интервале заключены все неэквивалентные значения волнового вектора .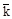

Аналогично тому, как была построена симметричная ячейка Вигнера–Зейтца, можно и в случае обратной решетки выделить область, обладающую полной симметрией обратной решетки. Для этого проведем из некоторого узла, выбранного за начальный, векторы 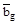ко всем ближайшим к нему узлам.

Через середины этих векторов проведем плоскости, перпендикулярные к ним. Уравнения этих плоскостей имеют вид

.

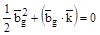Эти пересекающиеся плоскости образуют некоторые многогранники в обратном пространстве, называемые зонами Бриллюэна.

Из самого построения первой зоны Бриллюэна следует, что волновые векторы 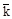, концы которых лежат внутри нее, отличаются друг от друга меньше, чем на вектор обратной решетки. Если же конец вектора 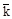лежит на границе зоны, то всегда существует, по крайней мере, один, эквивалентный вектор , конец которого также лежит на границе зоны.

Определим форму первой зоны Бриллюэна для решетки типа алмаза. Решетка типа алмаза состоит из двух гранецентрированных подрешеток. Обратное пространство для гранецентрированной структуры обладает симметрией объемно центрированного куба. Следовательно, каждый узел окружен восемью ближайшими узлами. Восемь плоскостей, проведенных через середины векторов, соединяющих начало координат с ближайшими узлами, – это плоскости {111}. Пересекаясь, они образуют правильный восьмигранник – октаэдр, с шестью вершинами в направлениях á100ñ и правильными треугольниками в виде граней {111}.

Узлами следующей координационной сферы являются шесть узлов в направлении á100ñ, шесть плоскостей, проведенных через середины векторов á100ñ перпендикулярно к ним, отсекут шесть вершин октаэдра, образуя шесть квадратных граней {100} зоны Бриллюэна. Таким образом, для первой зоны Бриллюэна получается четырнадцатигранник с шестью квадратными и восемью шестиугольными гранями (рис. 48).

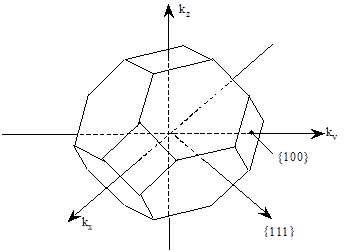
Рис. 48. Вид первой зоны Бриллюэна для решетки типа алмаза

Можно записать уравнения для граней первой зоны Бриллюэна. Полагая из построения обратной решетки для ГЦК структуры, получим следующее:

;

;

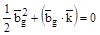или

.

Это уравнение определяет одну из восьми шестиугольных граней. Если , т. е. совпадает с направлением á100ñ, то получим , что определяет одну из шести квадратных граней.