 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Обратная решетка
|
|
При рассмотрении расположения атомов в кристалле было введено такое понятие, как решетка. Характеризуя симметрию расположения атомов в пространстве, мы пользуемся симметричными преобразованиями в прямом пространстве, пространстве, размерность которого [длина]3.
Чтобы можно было характеризовать симметрию физических свойств, вводят в рассмотрение представление об обратном пространстве и об обратной решетке. Соответственно размерность пространства при этом [длина]-3.
Главнейшим свойством идеального кристалла является периодическое расположение атомов в пространстве. Это означает, что при смещении всего кристалла в целом на вектор трансляции
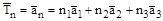
кристалл совмещается сам с собой.
Очевидно, что такие величины, как электростатический потенциал, плотность электронов, рассматриваемые в некоторой точке внутри кристалла, являются пространственно или трехмерно-периодическими функциями. Некоторая точка внутри кристалла, определяемая радиусом вектором 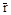 , и точка с радиусом вектором
, и точка с радиусом вектором 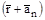 эквивалентны, поэтому электростатический потенциал в этих точках одинаков, т. е.
эквивалентны, поэтому электростатический потенциал в этих точках одинаков, т. е.
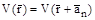 .
.
Эту трехмерно-периодическую функцию можно разложить в тройной ряд Фурье. Для разложения введем координаты x1, x2,x3 косоугольной системы координат, оси которой направлены по векторам 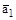 ,
, 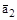 ,
,  . В этом случае функция
. В этом случае функция 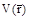 периодична в переменных xi (где i = 1, 2, 3) с периодами аj (j = 1, 2, 3).
периодична в переменных xi (где i = 1, 2, 3) с периодами аj (j = 1, 2, 3).
Разложение запишем в комплексной форме
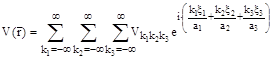 .
.
Перейдем от косоугольных координат xi к прямоугольным координатам хi:
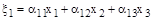 ;
;
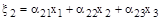 ;
;
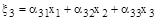 ,
,
где aik – коэффициенты, зависящие от углов между осями косоугольной и прямоугольной координатных систем. Подставим в выражение 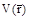 значение xi. Результат запишем в виде
значение xi. Результат запишем в виде
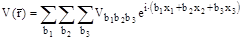 .
.
Здесь bi – это коэффициенты, зависящие от aik, ki, ai. Суммирование проводится по всем различным значениям величин bi, соответствующим всем целочисленным значениям индексов ki. Формально величины bi, полученные чисто математическим путем и не имеющие физического смысла, могут быть рассмотрены как прямоугольные компоненты некоего вектора 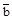 . И величину электростатического потенциала можно записать таким образом:
. И величину электростатического потенциала можно записать таким образом:
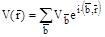 .
.
На вопрос, что же такое есть 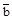 , проще всего ответить, обратившись к условию периодичности
, проще всего ответить, обратившись к условию периодичности 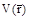 ,
,
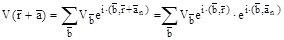 ;
;
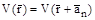 ,
,
получаем, что
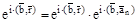 ,
,
т. е.
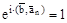 ,
,
а значит,
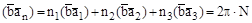 ,
,
где N – целое число.
Это возможно в том случае, когда
 ;
;
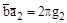 ; (*)
; (*)
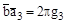 ,
,
g1, g2, g3 – произвольные целые числа, включая ноль.
Запомним эти соотношения, они понадобятся при рассмотрении дифракции излучения на кристаллической решетке.
Каждый вектор определяется тремя своими составляющими, поэтому этих трех независимых уравнений достаточно для определения вектора 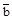 .
.
(Точно так же как для случая прямой решетки вводится вектор 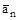 с индексом n, обозначающим те целые числа, которые входят в уравнение для
с индексом n, обозначающим те целые числа, которые входят в уравнение для 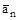 ,
, 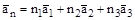 , для вектора
, для вектора 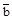 вводится индекс «g».)
вводится индекс «g».)
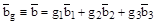 ;
;
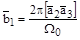
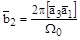
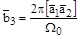 ,
,
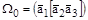 – объем элементарной ячейки прямой решетки.
– объем элементарной ячейки прямой решетки.
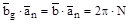 , где N – целое число.
, где N – целое число.
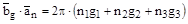 .
.
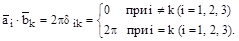
Векторы  носят название основных векторов обратной решетки. Они имеют размерность, обратную длине. Бесконечная периодическая решетка, построенная на векторах
носят название основных векторов обратной решетки. Они имеют размерность, обратную длине. Бесконечная периодическая решетка, построенная на векторах  как на векторах трансляции, представляет собой обратную решетку. Пространство обратной решетки имеет размерность [длина]-3. Параллелепипед, построенный на векторах
как на векторах трансляции, представляет собой обратную решетку. Пространство обратной решетки имеет размерность [длина]-3. Параллелепипед, построенный на векторах  , называется элементарной ячейкой обратной решетки.
, называется элементарной ячейкой обратной решетки.
Из определения векторов  видно, что
видно, что  перпендикулярен векторам
перпендикулярен векторам 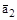 и
и  ; вектор
; вектор 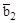 перпендикулярен векторам
перпендикулярен векторам 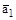 и
и  ; вектор
; вектор  перпендикулярен векторам
перпендикулярен векторам 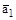 и
и 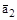 .
.
Следовательно, если элементарная ячейка прямой решетки имеет форму прямоугольного параллелепипеда, то вектора  ,
, 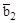 ,
,  параллельны векторам
параллельны векторам 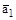 ,
, 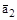 ,
,  .
.
Представление об обратной решетке используется для описания симметрии физических свойств, при изучении движения электронов в периодическом поле, при исследовании колебания атомов в кристалле, при изучении дифракции рентгеновских лучей и т.п.
Рассмотрим два важных положения, относящихся к обратной решетке.
1. Вектор обратной решетки
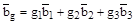
перпендикулярен плоскости (hkl), если выполняется соотношение между индексами плоскости и целыми числами gi такое, что

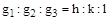 .
.
|
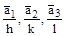 . Вектора
. Вектора 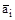 представляют собой основные вектора трансляций вдоль соответствующих координат (рис. 45). Концы векторов
представляют собой основные вектора трансляций вдоль соответствующих координат (рис. 45). Концы векторов 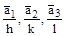 лежат на плоскости (hkl), поэтому векторы, представляющие разность этих векторов, т. е.
лежат на плоскости (hkl), поэтому векторы, представляющие разность этих векторов, т. е. 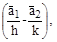
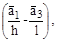 лежат в плоскости (hkl).
лежат в плоскости (hkl).Рассмотрим вектор 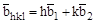 + +
+ + 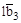 , если выполняется cоотношение
, если выполняется cоотношение  , вектор
, вектор 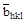 будет параллелен вектору
будет параллелен вектору 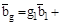
+ 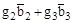 ;
; 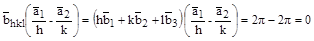 ;
; 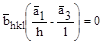 , этот результат говорит о том, что вектор
, этот результат говорит о том, что вектор  перпендикулярен двум векторам, лежащим в плоскости (hkl), следовательно, он перпендикулярен самой плоскости (hkl). Но было установлено, что
перпендикулярен двум векторам, лежащим в плоскости (hkl), следовательно, он перпендикулярен самой плоскости (hkl). Но было установлено, что  параллелен вектору
параллелен вектору 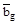 , значит, вектор
, значит, вектор 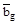 перпендикулярен плоскости (hkl).
перпендикулярен плоскости (hkl).
2. Расстояние между соседними плоскостями семейства параллельных плоскостей {hkl} определяется выражением
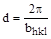 .
.
Введем в рассмотрение 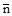 – единичный вектор нормали к параллельным плоскостям (hkl)
– единичный вектор нормали к параллельным плоскостям (hkl)
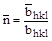 ;
; 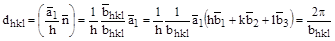 .
.
Параллелепипед, построенный в обратном пространстве на векторах  ,
, 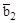 ,
,  , не обладает симметрией обратной решетки. Но можно при рассмотрении обратного пространства выделить область, обладающую полной симметрией обратной решетки. Для этого необходимо построить ячейку Вигнера–Зейтца в обратном пространстве. Ячейка Вигнера–Зейтца в обратном пространстве носит название зоны Бриллюэна. Правило построения ячейки Вигнера–Зейтца таково: необходимо выбрать какой-либо узел в качестве начального узла. Из этого узла проводятся вектора в направлении ближайших к нему узлов, к так называемым узлам первой координационной сферы. Через середины этих векторов проводятся плоскости, перпендикулярные к ним. Область пространства, ограниченная этими плоскостями, и есть ячейка Вигнера–Зейтца. Этими ячейками можно заполнить все пространство кристалла. Зона Бриллюэна представляет собой минимальную область обратного пространства (или фазового пространства, или пространства обратных волновых чисел), в которой волновая функция электрона пробегает все возможные допустимые значения.
, не обладает симметрией обратной решетки. Но можно при рассмотрении обратного пространства выделить область, обладающую полной симметрией обратной решетки. Для этого необходимо построить ячейку Вигнера–Зейтца в обратном пространстве. Ячейка Вигнера–Зейтца в обратном пространстве носит название зоны Бриллюэна. Правило построения ячейки Вигнера–Зейтца таково: необходимо выбрать какой-либо узел в качестве начального узла. Из этого узла проводятся вектора в направлении ближайших к нему узлов, к так называемым узлам первой координационной сферы. Через середины этих векторов проводятся плоскости, перпендикулярные к ним. Область пространства, ограниченная этими плоскостями, и есть ячейка Вигнера–Зейтца. Этими ячейками можно заполнить все пространство кристалла. Зона Бриллюэна представляет собой минимальную область обратного пространства (или фазового пространства, или пространства обратных волновых чисел), в которой волновая функция электрона пробегает все возможные допустимые значения.
Прежде чем перейти к рассмотрению закономерностей построения зоны Бриллюэна для важнейших полупроводниковых материалов, рассмотрим построение обратной решетки для случая, когда прямая решетка обладает симметрией объемно центрированного куба или ОЦК и гранецентрированного куба или ГЦК.
Дата публикования: 2014-11-18; Прочитано: 1019 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
