Примеры некоторых статистических распределений

В измерительной практике при обработке результатов эксперимента в качестве статистических моделей наиболее часто, применяются два вида распределений случайной величины: нормальное (гауссово) и равномерное (прямоугольное) [10], [12], [17], [40], [51]. Нормальное распределение, как правило, применяется при обработке результатов многократных независимых наблюдений и расчете приборной погрешности. Равномерное распределение используется в качестве статистической модели при расчете погрешностей округления и отсчета.

2.3.1. Случайная величина называется распределенной нормально, если функция плотности распределения вероятностей имеет вид:

(23),

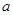где и 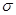– параметры распределения.

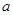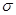Вероятностный смысл параметров и состоит в том, что параметр 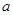является математическим ожиданием , параметр 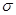– среднее квадратическое отклонение 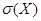[10].

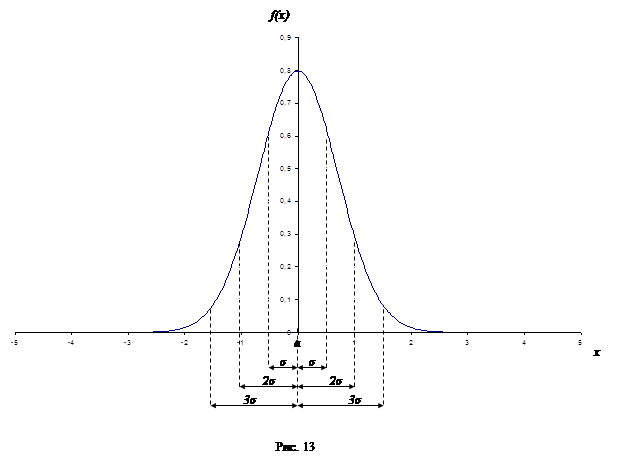График функции плотности вероятностей нормально распределенной величины представляет собой колоколообразную кривую (рис. 13). Параметр 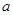– точка максимума, через которую проходит ось симметрии, параметр 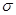– расстояние от оси симметрии до точки перегиба на кривой. Если 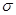мало, то кривая высокая и заостренная, если велико, то она широкая и плоская.

Характерной особенностью нормального распределения является то, что для него математическое ожидание, медиана и мода совпадают, причем:

§ вероятность попадания случайной величины Х в интервал составляет 68%, т. е. ,

§ вероятность попадания случайной величины Х в интервал 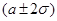оставляет 95%, т. е. ,

§ вероятность попадания случайной величины Х в интервал составляет 99,7%, т. е. 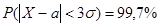(рис.13).

Последнее выражение, называют «правилом трех сигм». Вероятность того, что абсолютная величина отклонения случайной величины от математического ожидания превысит утроенное среднее квадратическое отклонение, очень мала и составляет приблизительно 0,27%. Такие события, можно считать практически невозможными. В этом и состоит сущность правила трех сигм: если величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

Кроме того, если случайная величина распределена по нормальному закону, то ее среднее квадратическое отклонение 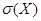и среднее отклонение связаны соотношением:

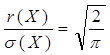(24).

Во многих задачах 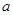и 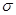неизвестны и должны оцениваться на основе имеющихся экспериментальных данных.

Пусть серия результатов является случайной выборкой объема n из совокупности значений, подчиняющихся нормальному распределению, тогда:

а). Точечная оценка математического ожидания (выборочное среднее см. формулу 19) есть среднее арифметическое элементов выборки:

(25).

В измерительной практике выборочное среднее 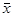принимается за результат измерения. Это означает, что в качестве истинного значения измеряемой величины берется математическое ожидание нормально распределенной генеральной совокупности. Данное утверждение составляет основу математической обработки результатов наблюдений при измерении. Поэтому для получения верной оценки истинного значения измеряемой величины очень важно, чтобы выборка – результаты наблюдений при измерении – принадлежала нормальному распределению. Точность оценки тем выше, чем больше объем выборки.

Неточность соответствия выборочного (эмпирического) среднего истинному значению измеряемой величины определяется:

§ выборочным средним абсолютным отклонением (точечной оценкой среднего абсолютного отклонения см. формулу 20)

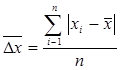(26),

которое в измерительной практике называется средней арифметической погрешностью;

§ выборочным средним квадратическим отклонением (точечной оценкой среднего квадратического отклонения см. формулу 22):

(27),

которое в измерительной практике называется средней квадратической погрешностью результата наблюдения [6], [18], [43].

Для нормального распределения выборочное среднее 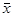также распределено нормально, причем выборочное среднее квадратическое отклонение среднего арифметического (см. формулу 15)определяется по формуле:

(28),

которое в измерительной практике называется средней квадратической погрешностью результата измерения [43].

Примечание. Так как средняя арифметическая погрешность и средняя квадратическая погрешность S являются оценками среднего отклонения и среднего квадратического отклонения 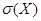соответственно, то на основании формулы (24), можно считать, что данные погрешности должны быть связаны между собой приближенным соотношением:

(29).

б). Интервальная оценка математического ожидания задается в виде доверительного интервала [6], [10], [16]:

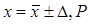(30), где

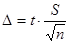§ при объеме выборки n >30. Число t определяется из равенства 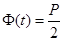, по таблице функции Лапласа [10] находят аргумент t, которому соответствует значение функции Лапласа, равное ;

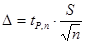§ при объеме выборки n ≤30. Число 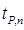– этокоэффициент Стьюдента для объема выборки n и доверительной вероятности Р.

Наиболее часто используются следующие значения доверительной вероятности Р: 0,95; 0,997. Если Р = 0,997, то доверительный интервал принимается за максимальный. Смысл соотношения (30) состоит в следующем: с вероятностью Р можно утверждать, что доверительный интервал (30) покрывает истинное значение измеряемой величины Х. Другими словами оценка истинного значения неизвестного параметра в виде доверительного интервала означает, что если имеется достаточно большое число выборок, то Р из них определяет такие доверительные границы, в которых действительно заключено истинное значение неизвестного параметра, и только в 1- Р случаях он может выйти за границы доверительного интервала [10].

В измерительной практике 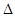– называют доверительной границей случайной погрешности результата измерения [12].

2.3.2. Случайная величина Х называется равномерно распределенной на интервале , которому принадлежат все возможные значения этой величины,если плотность распределения вероятностей на интервале сохраняет постоянное значение, а вне интервала равна нулю:

(31).

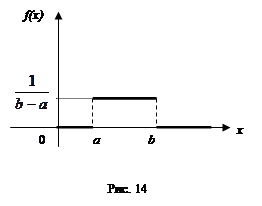
На рис. 14 изображен график функции плотности вероятностей равномерного распределения. Для равномерного (прямоугольного) распределения математическое ожидание и среднее квадратическое отклонение 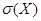рассчитываются по следующим формулам:

; (32).

Доверительная граница случайной погрешности результата измерения [18], [41]: 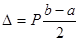(33).

2.3.3. Если функция плотности распределения вероятностей и дисперсия случайной величины неизвестны, то для оценки математического ожидания можно построить ориентировочный интервал для выборки объем, которой 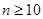(используя неравенство Чебышева см. [10], [17], [51]):

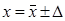, Р (34),

, где 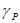– коэффициент для неравенства Чебышева при объеме выборки 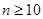и ориентировочной вероятности Р (доверительная вероятность лишь ориентировочно равна Р, т. е. может быть несколько больше или несколько меньше).

Примечание. При вычислении интервала вида (34) не следует использовать значения Р, близкие к единице, так как в этом случае погрешность особенно велика. Целесообразно использовать значения Р в пределах около от 0,6 до 0,8.

Если же объем выборки 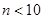, то вычислять ориентировочный интервал не имеет смысла, в этом случае лучше привести выборочные характеристики: 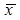, , 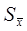n.