Выборочный метод

Выборочным методом называют метод исследования общих свойств совокупности каких-либо объектов на основе изучения свойств лишь части этих объектов, взятых на выборку [5], [10].

Выборкой или выборочной совокупностью называют совокупность случайно отобранных объектов. Все множество однородных объектов, из которых производится выборка, называют генеральной совокупностью.

Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности.

Пусть для изучения признака Х из генеральной совокупности извлечена выборка 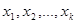. Причем 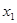наблюдалось раз, 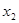– 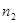раза и т. д., и – объем выборки. Наблюдаемые значения признака Х называют вариантами, а последовательность вариант, записанных в возрастающем порядке, называют вариационным рядом [10].

Число наблюдений появления значения называют частотой появления этого значения. Сумма всех частот равна объему выборки:

(16).

Относительной частотой появления значения называют отношение частоты к объему выборки n:

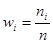(17).

Сумма всех относительных частот равна единице: .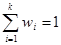

Примечание. Расчетные формулы для нахождения вероятности 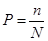(формула 7) и относительной частоты 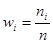(формула 17) похожи. Отличие относительной частоты от вероятности заключается в том, что вероятность задают до опыта, а относительную частоту вычисляют по фактическим результатам опыта. Если опытным путем установлена относительная частота, то полученное число можно принять за приближенное значение вероятности.

Статистическим распределением выборки, называют перечень вариант вариационного ряда и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот. В качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал. Поскольку статистическое распределение выборки находят по эмпирическим (опытным) данным его иногда называют эмпирическим распределением.

Эмпирическое распределение может быть задано через эмпирическую функцию распределения.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию 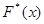, определяющую для каждого значения х относительную частоту события :

,

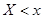где 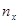– число вариант, меньших х,

– объем выборки.

Эмпирическая функция распределения служит для оценки функции распределения вероятностей.

Для графического представления непрерывно распределенной случайной величины, как правило, строят гистограмму относительных частот, которая дает возможность оценить плотность распределения вероятностей.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною , а высоты определяются формулой:

(18),

где – сумма частот попадания значения в заданный интервал значений ,

– объем выборки.

Методы математической статистики дают возможность по результатам выборки найти приближенные значения математического ожидания, медианы и моды, которые называются оценками координат центра распределения, а также приближенные значения среднего отклонения и среднего квадратического отклонения, которые называются оценками среднего отклонения и среднего квадратического отклонения [10], [51], [55]:

1. Оценка математического ожидания. В качестве оценки математического ожидания 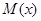принимается выборочное (эмпирическое) среднее , которое вычисляют как среднее арифметическое всех элементов выборки:

(19).

2. Оценка медианы. Элементы выборки представляют в виде вариационного ряда. Если число n элементов выборки нечетное, то оценка медианы 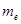равна значению 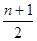упорядоченного элемента выборки, т.е. ; если n – четное число, то оценка медианы 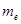равна среднему арифметическому значению между 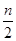и 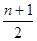упорядоченными элементами выборки, т. е. .

3. Оценка моды. В качестве оценки моды выбирается элемент выборки (результат наблюдения), который встречается наиболее часто. В некоторых случаях целесообразно сгруппировать данные по интервалам частот одинаковой длины. При этом мода берется как центральная точка частотного интервала, содержащего наибольшее число элементов выборки.

4. Оценка среднего отклонения. В качестве оценки среднего отклонения принимается величина , которая называется средним абсолютным отклонением:

(20).

5. Оценка дисперсии. В качестве оценки дисперсии D(X) принимается выборочная дисперсия 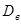, которая вводится для того, чтобы охарактеризовать рассеяние элементов выборки вокруг выборочного среднего:

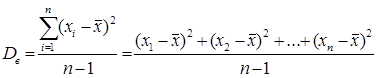, n 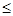30 (21).

6. Оценка среднего квадратического отклонения. В качестве оценки среднего квадратического отклонения 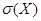принимается выборочное среднее квадратическое отклонение (эмпирический стандарт) , которое находится как квадратный корень из выборочной дисперсии:

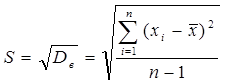, n 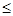30 (22).

Оценка параметров распределения случайной величины может быть точечной или интервальной [6], [10], [16].

Точечной оценкой называют оценку, которая определяется одним числом. В частности, значение выборочного среднего, рассчитанного по формуле (19), называется точечной оценкой математического ожидания; выборочное среднее квадратическое отклонение, рассчитанное по формуле (22) – это точеная оценка среднего квадратического отклонения.

При малом объеме выборки точечная оценка может значительно отличаться от оцениваемого параметра, по этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.

Пусть по данным выборки найдена оценка 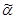параметра 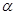. Данная оценка тем точнее, чем меньше абсолютная величина разности 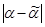. Положительное число 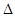такое, что 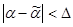характеризует точность оценки, чем меньше 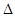, тем оценка точнее. Однако статистические методы не позволяют категорически утверждать, что оценка 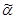удовлетворяет неравенству 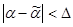; можно лишь говорить о вероятности, с которой это неравенство выполняется. Доверительной вероятностью (надежностью) оценки называют вероятность Р, с которой выполняется неравенство 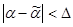или равносильное ему двойное неравенство .

Интервальная оценка состоит в определении по данной выборке границ интервала 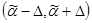, который с заданной доверительной вероятностью Р заключает в себе (покрывает) неизвестный параметр 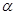. Данный интервал называют доверительным. Концы доверительного интервала называются доверительными границами, которые, вообще говоря, зависят от следующих факторов:

§ вида статистического распределения генеральной совокупности;

§ доверительной вероятности Р;

§ объема выборки n.

Итак, по выборке можно оценить координаты центра распределения случайной непрерывной величины: математическое ожидание, медиану и моду, а также показатель рассеяния относительно среднего: выборочное среднее квадратическое и выборочное среднее отклонения.