Некоторые сведения из теории вероятностей

И математической статистики

Теория вероятностей и математическая статистика – разделы математики, тесно связанные друг с другом. В теории вероятностей на основе принятой статистической модели рассчитываются вероятности появления случайных событий. В математической статистике на основе экспериментальных данных формулируют гипотезу о принадлежности данной выборки к той или иной вероятностной модели, проверяют ее и на основе выбранной статистической модели описывают результаты наблюдений. Статистическое описание и вероятностные модели в настоящее время применяются в экспериментальных исследованиях по физике. Рассмотрим некоторые понятия теории вероятностей и математической статистики, которые используются при математической обработке экспериментальных данных [6], [10], [16], [51], [55].

Основные понятия теории вероятностей

В теории вероятностей наблюдаемые явления называются событиями. События могут быть достоверными, невозможными и случайными. Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий. Невозможным событием называют событие, которое заведомо не произойдет, если будет осуществлена некоторая совокупность условий. Случайным называют событие, которое при осуществлении совокупности некоторых условий может либо произойти, либо не произойти.

Количественной оценкой объективной возможности появления данного события является вероятность Р события, которая математически определяется отношением числа n случаев, благоприятствующих событию к общему числу N всех возможных случаев [10]:

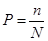(7).

Из (7) следует:

§ вероятность достоверного события (n=N) всегда равна единице: P=1;

§ вероятность невозможного события (n=0) всегда равна нулю: P=0;

§ вероятность случайного события (n<N) всегда выражается правильной дробью: .

Случайной величиной называется величина, которая в зависимости от случая принимает различные значения. Случайные величины могут быть дискретными и непрерывными. Дискретной (прерывной) называют случайную величину, которая принимает конечное или счетное число значений. Примером дискретной случайной величины может служить число попаданий в цель при данном количестве выстрелов. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. В отличие от дискретных, непрерывные случайные величины могут принимать любое значение.

Результаты измерений значений физических величин относятся к непрерывным случайным величинам.

Поэтому остановимся подробнее на непрерывных случайных величинах [10].

Рассмотрим непрерывную случайную величину Х, возможные значения которой сплошь заполняют интервал (а, b). В данном случае составить перечень всех возможных значений величины Х нельзя. Для задания такого вида случайной величины вводят функцию распределения вероятностей случайной величины.

Пусть х – действительное число. Вероятность события, состоящего в том, что случайная величина Х примет значение, меньшее х, т. е. вероятность события Х<x, обозначим через F(x). Если х изменяется, то, вообще говоря, изменяется и F(x), т.е. F(x) является функцией от х.

Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т.е. [6], [10], [16].

Непрерывную случайную величину можно задать, используя другую функцию, которую называют плотностью распределения вероятностей или плотностью вероятностей.

Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) равную первой производной от функции распределения F(x),т. е. 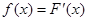. По определению:

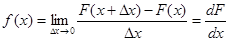(8).

Следовательно 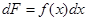и если значения непрерывной случайной величины Х распределены в интервале (a, b), то

.

Так как 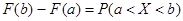, то вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b [10]:

.

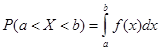Геометрически полученный результат можно трактовать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью Ох, кривой плотности распределения вероятностей f(x) и прямыми х=а и х=b (рис.10).

Плотность распределения вероятностей f(x) непрерывной случайной величины называют также законом распределения. Наиболее часто используются законы нормального и равномерного распределений (см. п. 2.3, § 2, гл. 3, раздел I).

Одной из наиболее важных характеристик функции f(x) является точка, вокруг которой группируется распределение – центр распределения. Если известно аналитическое выражение функции плотности распределения вероятностей (8), то задать центр распределения можно тремя способами, вычислив:

1. Математическое ожидание М(Х), которое определяется по формуле:

(9).

2. Медиану Ме, т. е. значение абсциссы 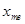такой точки кривой плотности распределения вероятностей f(x), которая делит пополам площадь под кривой плотности распределения. Значение медианы можно найти из уравнения:

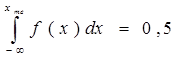(10).

3. Моду Мо, т. е. значение абсциссы точки кривой плотности распределения вероятностей f(x), при котором f(x) достигает максимума. Если функция f(x) имеет один максимум, то называют наиболее вероятным значением случайной величины.

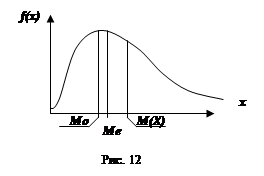
Математическое ожидание, медиана и мода могут совпадать в случае, если функция f(x) симметричная (рис. 11). Если функция f(x) не является симметричной, то математическое ожидание, медиана и мода не совпадают (рис. 12).

Кроме центра распределения часто бывает необходимо описать рассеяние случайной величины относительно математического ожидания. Для числовой характеристики рассеяния случайной величины используют:

1. Среднее отклонение r(X) случайной величины Х от ее математического ожидания, которое для случайной непрерывной величины определяется по формуле:

(11).

2. Дисперсию D(X), которая для случайной величины Х представляет собой математическое ожидание квадрата ее отклонения и определяется по формуле:

(12).

3. С реднее квадратическое отклонение 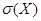случайной величины Х, которое представляет собой квадратный корень из дисперсии и определяется по формуле:

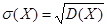(13).

Примечание 1. Если случайная величина Х представляет собой сумму случайных величин Х₁, Х₂, …, Х_n, которые имеют разные распределения, то в этом случае, среднее квадратическое отклонение данной величины равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:

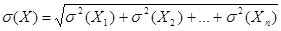(14).

Примечание 2. Если имеется n взаимно независимых случайных величин Х₁, Х₂, …, Х_n, которые имеют одинаковые распределения, а следовательно, и одинаковые характеристики (математическое ожидание, дисперсию и т.д.), то среднее квадратическое отклонение среднего арифметического в 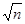раз меньше среднего квадратического отклонения 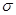каждой из величин:

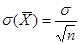(15),

где .