Решение задач

Задача 2.6. Найти поток векторного поля через часть плоскости , ограниченную координатными плоскостями, и плоскостью 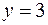в направлении нормали, образующей тупой угол с осью .

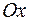Решение. Для вычисления потока воспользуемся формулой (2.10), вычислив предварительно . Так как рассматриваемая поверхность - плоскость, то коэффициентами перед переменными являются координаты нормали к ней, т.е. 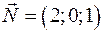. Соответственно единичная нормаль 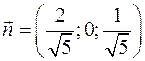. Тогда

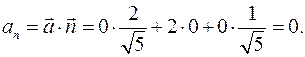
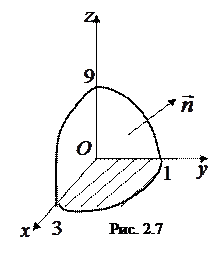Следовательно,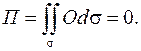

Задача 2.7. Найти поток векторного поля 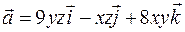через часть поверхности 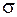: , лежащую в первом октанте 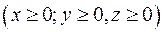в направлении нормали, образующей острый угол с осью .

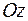Решение. Для вычисления потока будем использовать формулу (2.12), вычислив предварительно величины, входящие в нее.

Выразим из уравнения поверхности: 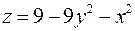. Тогда ,

, , .

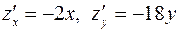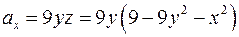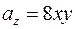Тогда в соответствии с формулой (8.12) получаем

Область 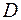, проекция рассматриваемой части поверхности 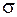на плоскость (на рис. 2.7 заштрихована), ограничена осями координат и кривой, уравнение которой 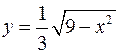получено из уравнения поверхности при . Тогда

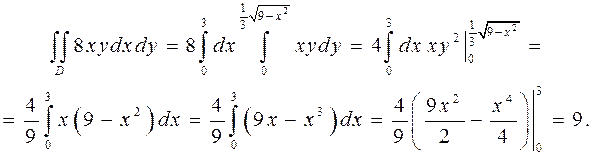
Задача 2.8. Вычислить с помощью теоремы Остроградского-Гаусса поток векторного поля 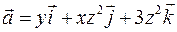в сторону внешней нормали через полную поверхность 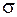тела, лежащего в первом октанте 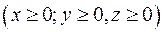, и ограниченного поверхностью 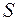: 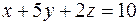и координатными плоскостями.

Решение. Вычислим дивергенцию векторного поля, используя формулу (8.13).

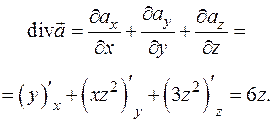
Тогда в соответствии с формулой (2.14)

.

Перейдем от тройного интеграла к повторному, используя вид области (рис. 2.8).

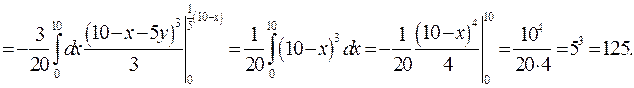
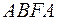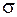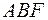Задача 2.9. Вычислить, используя определение, циркуляцию векторного поля по линии пересечения с координатными плоскостями части поверхности : , лежащей в первом октанте, - точки пересечения поверхности с осями соответственно.

Решение. Рассматриваемая кривая изображена на рис. 2.9. Используя определение циркуляции и свойство аддитивности криволинейного интеграла, получаем

Вычислим отдельно каждый из трех интегралов.

1) На дуге 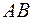и 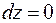, поэтому .

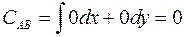2) Дуга 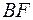является частью параболы , а меняется от 1 до 0. Учитывая, что и 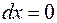, получаем

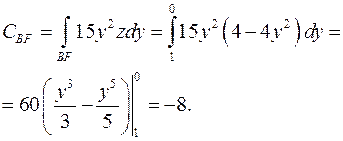
3) Дуга 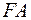- часть параболы 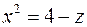, 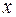меняется от 0 до 2. Учитывая, что 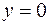и 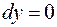, получаем

.

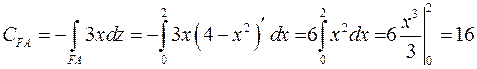Суммируя полученные результаты, получаем .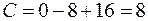

Задача 8.10. Используя теорему Стокса, вычислить циркуляцию векторного поля по линии 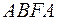, линии пересечения с координатными плоскостями той части поверхности : 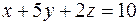, которая лежит в первом октанте; 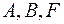- точки пересечения поверхности с осями соответственно (рис. 2.10).

Решение. Вычислим , используя формулу (2.19):

Тогда , и в соответствии с формулой Стокса (2.17) получаем

.

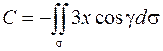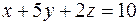В качестве поверхности берем плоскость . Заданному направлению обхода контура 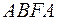соответствует нормаль, образующая острый угол с осью 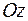. Следовательно,

,

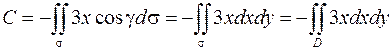где 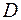- проекция 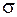на плоскость . Используя вид области 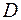(рис. 2.10), перейдем к повторному интегралу и вычислим его.

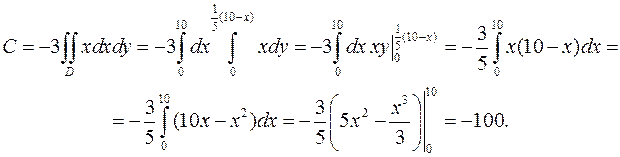
Вопросы для самопроверки по теме 2.2

1. Что такое векторное поле?

2. Дайте определение векторной линии, векторной поверхности.

3. Какая физическая задача приводит к понятию потока векторного поля?

4. Дайте определение потока векторного поля через заданную поверхность.

5. Что такое дивергенция векторного поля?

6. Сформулируйте теорему Остроградского-Гаусса в векторной форме.

7. Дайте определение циркуляции и ротора векторного поля.

8. Сформулируйте теорему Стокса в векторной форме.