 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Циркуляция и ротор векторного поля. Теорема Стокса в векторной форме
|
|
Пусть в некоторой области  задано векторное поле
задано векторное поле
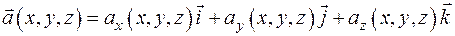 .
.
Пусть далее 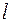 - кривая, лежащая в области
- кривая, лежащая в области  .
.
Интеграл 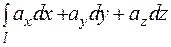 называется линейныминтегралом поля
называется линейныминтегралом поля  по кривой
по кривой 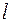 . Этот интеграл иногда обозначают так:
. Этот интеграл иногда обозначают так: 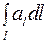 .
.
Если кривая 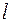 - замкнутая, то такой интеграл называется циркуляцией поля
- замкнутая, то такой интеграл называется циркуляцией поля  вдоль кривой
вдоль кривой 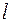
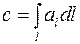
Если поле  -силовое поле, то линейный интеграл выражает работу сил поля при перемещении точки единичной массы по кривой
-силовое поле, то линейный интеграл выражает работу сил поля при перемещении точки единичной массы по кривой 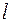 .
.
Пусть в области  задана гладкая двусторонняя поверхность
задана гладкая двусторонняя поверхность 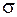 , ограниченная замкнутым контуром
, ограниченная замкнутым контуром 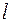 . Тогда, используя формулу Стокса и формулу перехода от поверхностного интеграла второго рода к интегралу первого рода, можно вычислить циркуляцию
. Тогда, используя формулу Стокса и формулу перехода от поверхностного интеграла второго рода к интегралу первого рода, можно вычислить циркуляцию  так:
так:
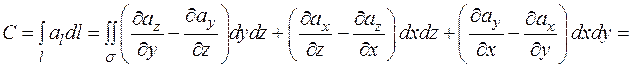
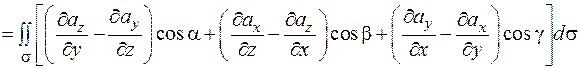 .(2.15)
.(2.15)
Последний интеграл равен потоку векторного поля, которая называется ротором или вихрем поля  и обозначается символом
и обозначается символом
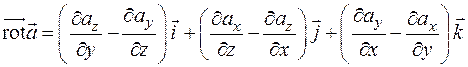 . (2.16)
. (2.16)
Тогда равенство (2.15) можно записать в виде
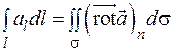 . (2.17)
. (2.17)
Таким образом, теорему Стокса можно сформулировать в векторной форме.
Циркуляция поля  вдоль замкнутого контура
вдоль замкнутого контура  равна потоку ротора этого поля через поверхность
равна потоку ротора этого поля через поверхность 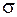 ,ограниченную контуром
,ограниченную контуром 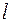 . При этом сторона поверхности и направление обхода должны соответствовать друг другу.
. При этом сторона поверхности и направление обхода должны соответствовать друг другу.
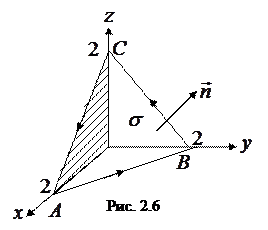 Пример 2.9. Вычислить, используя теорему Стокса, циркуляцию поля
Пример 2.9. Вычислить, используя теорему Стокса, циркуляцию поля 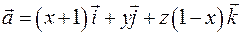 по линии
по линии 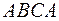 пересечения плоскости
пересечения плоскости 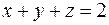 скоординатными плоскостями. Точки
скоординатными плоскостями. Точки 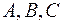 - точки пересечения плоскости с осями
- точки пересечения плоскости с осями  соответственно.
соответственно.
Решение. Вычислим сначала частные производные, участвующие в определении ротора (2.16).
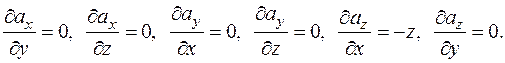
Тогда 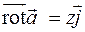 , и, значит,
, и, значит, 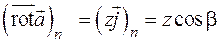 . Используя формулу Стокса (2.17), получаем
. Используя формулу Стокса (2.17), получаем
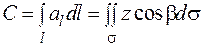 . (2.18)
. (2.18)
|
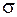 берем плоскость
берем плоскость 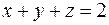 . Заметим, что заданному направлению обхода контура соответствует нормаль, образующая острыйугол с осью
. Заметим, что заданному направлению обхода контура соответствует нормаль, образующая острыйугол с осью 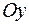 ,т.е.
,т.е. 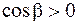 . Перейдем от поверхностного интеграла в равенстве (2.18) к двойному, проектируя поверхность
. Перейдем от поверхностного интеграла в равенстве (2.18) к двойному, проектируя поверхность 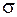 на плоскость
на плоскость 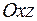 (проекция
(проекция 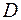 на рис. 2.6 заштрихована). Так как
на рис. 2.6 заштрихована). Так как 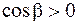 , то
, то 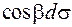 заменим на
заменим на  . Вычислим двойной интеграл:
. Вычислим двойной интеграл:
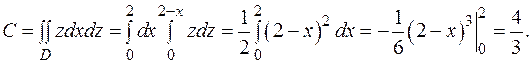
Примечание. Вычисление ротора векторного поля
Ротор векторного поля  (2.16) удобно вычислять, используя формулу
(2.16) удобно вычислять, используя формулу
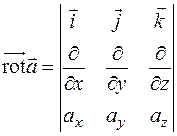 . (2.19)
. (2.19)
Этот определитель вычисляется по обычным правилам вычисления определителей, только формальное умножение любого из символов 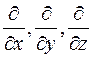 на
на  надо понимать, как взятие частной производной.
надо понимать, как взятие частной производной.
Пример 2.10. Вычислить ротор векторного поля 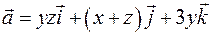 .
.
Решение. Воспользуемся формулой (8.19). Вычислять определитель будем, раскладывая его по первой строке,
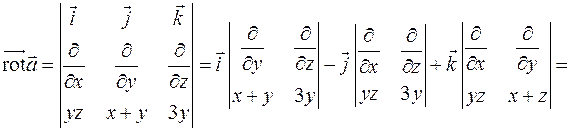
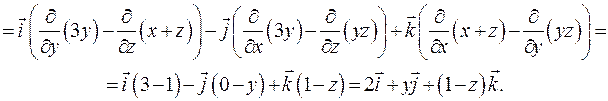
Дата публикования: 2014-11-19; Прочитано: 2030 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
