Цепях с сосредоточенными параметрами

КЛАССИЧЕСКИЙ МЕТОД РАСЧЁТА ПП

Общие положения

Если электрическая цепь достаточно долго сохраняла неизменный вид, то в ней создаётся так называемый установившийся (принуждённый) режим. Последнему соответствуют определённые законы изменения энергии элект-рических полей конденсаторов и магнитных полей индуктивностей цепи. В случае изменения схемы при переключениях, которые будем называть коммутациями, энергия полей должна измениться, а для этого требуется некоторое время. Процесс, возникающий в электрической цепи при переходе от одного установившегося режима к другому, называется переходным.

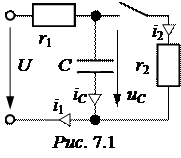
На протяжении ПП электрическая цепь может быть описана системой динамических уравнений, которая может быть сведена относительно одной электрической величины (тока или напряжения) к дифференциальному уравнению n- го порядка, причём его порядок определяется количеством накопителей энергии (к ним относятся индуктивности и ёмкости). Возникающее дифференциальное уравнение является линейным, неоднородным, с постоянными коэффициентами (см. задачу 7.1).

Общее решение полученного неоднородного линейного дифуравнения представляет собой сумму двух величин: частного решения неоднородного уравнения, выражающего принуждённый режим, задаваемый источниками, и решения соответствующего однородного дифуравнения, выражающего свободный режим.

В соответствии с этим для любого тока или напряжения можно записать: i = i_пр + i_св, u = u_пр + u_св,

где i_пр, u_пр – принуждённые составляющие тока и напряжения;

i_св, u_св – свободные составляющие тока и напряжения.

Метод нахождения электрических величин в виде суммы двух рассмотренных составляющих называется классическим.

Принуждённые составляющие рассчитываются любыми ранее изученными методами, а вид свободных составляющих зависит от числа и вида корней характеристического уравнения. Существует несколько способов составления характеристического уравнения.

1 способ. По имеющемуся дифференциальному уравнению:

K_n · 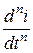+ K_{n -1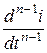}· + … + K ₁· + K ₀· i = f(t).

n -я производная заменяется на pⁿ;...; первая производная на p; сама величина – 1; правая часть – 0, то есть

K_n · pⁿ + K_{n -1}· p^{n -1} +... + K ₁· p + K ₀ = 0.

2 способ. Путём записи входного сопротивления в операторной форме:

1. Источники заменяются их внутренними сопротивлениями, а ключ показывается в послекоммутационном состоянии.

2. Цепь размыкается в любом месте. Рекомендуется разрывать в ветви с конденсатором, а при его отсутствии – в ветви с индуктивностью.

3. Относительно полученных зажимов записывается входное сопротивле-ние в комплексной форме Z (jw) (индуктивное сопротивление – jwL, а ёмкостное – 1/ (jwС)).

4. Производится замена jw = p. Получаем входное сопротивление Z(p) в операторной форме.

5. Полученное сопротивление приравниваем к нулю, т.е. Z(p) = 0. Это и есть характеристическое уравнение.

3 способ. Используя систему динамических уравнений цепи:

1. Составляется система динамических уравнений по законам Кирхгофа для послекоммутационного состояния цепи.

2. Полученная система алгебраизируется (из дифференциальных уравнения превращаются в алгебраические в операторной форме).

3. Определитель системы приравнивается к нулю и получается характеристическое уравнение.

Если корень характеристического уравнения один (обязательно отрицательный), свободная составляющая имеет вид: i_св(t) = A · e^pt,

где A – постоянная интегрирования;

Если корней два, оба действительные, отрицательные, разные, причём | p ₁| < | p ₂|, то i_св(t) = A ₁· 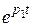+ A ₂· .

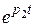Если корней два – действительные, отрицательные, равные (p ₁ = р ₂ = р), то i_св(t) = A ₁· e^pt + A ₂· t · e^pt,

где A ₁ и A ₂ – две постоянные интегрирования;

Если корней два – комплексные, сопряжённые, т.е. p _1,2 = - b ± jw ₀, то

i_св(t) = A · e^-bt · sin(w ₀ t + y),

где A и y – постоянные интегрирования.

Количество корней характеристического уравнения определяет число постоянных интегрирования и равно количеству накопителей энергии в цепи после коммутации.

Постоянные интегрирования находятся из начальных условий (значения электрических величин и их производных в начальный момент после коммутации), которые делятся на независимые и зависимые. К независимым относятся значения в момент коммутации потокосцепления и тока индуктивности, заряда и напряжения конденсатора. Остальные начальные условия считаются зависимыми.

Высказанные выше положения о том, что запас энергии магнитного или электрического поля может изменяться только плавно, без скачков, выра-жают принцип непрерывности во времени потокосцепления индуктивности и электрического заряда ёмкости и называются законами коммутации.

Первый закон коммутации: в индуктивном элементе ток и магнитный поток непосредственно после коммутации сохраняют значения, которые они имели непосредственно перед коммутацией, и дальше начинают изменяться

именно с этих значений: Y( 0₊ ) = Y( 0_- ), i_L( 0₊ ) = i_L( 0_- ),

где t = 0₊ – момент сразу после коммутации,

t = 0_- – момент непосредственно перед коммутацией.

Второй закон коммутации: на ёмкостном элементе напряжение и заряд сохраняют в момент коммутации те значения, которые они имели непосредственно перед коммутацией, и в дальнейшем изменяются, начиная с этих значений: q( 0₊ ) = q( 0_-), u_C( 0₊ ) = u_C( 0_- ).

При нулевых начальных условиях (i_L( 0_- ) = 0, u_C( 0_- ) = 0) индуктивность в начальный момент после коммутации равносильна разрыву цепи, а ёмкость – короткому замыканию. В случае ненулевых начальных условий (i_L( 0_- ) ¹ 0, u_C( 0_- ) ¹ 0) индуктивность в момент t = 0₊ равносильна источнику тока, а ёмкость – источнику ЭДС.

В зависимости от порядка дифуравнений различают цепи первого, второго и более высокого порядка.

Сущность классического метода анализа ПП показана на примере зада-чи 7.1. Однако применен нерациональный порядок расчёта. Рекомендуется следующий порядок расчёта ПП:

1. Анализом цепи до коммутации определение независимых начальных условий.

2. Запись искомых электрических величин (токов и напряжений) в виде суммы двух составляющих – принуждённой и свободной.

3. Расчёт принуждённых составляющих.

4. Вид свободных составляющих зависит от числа и вида корней характеристического уравнения. Поэтому тем или иным способом составляется и решается характеристическое уравнение.

5. Запись свободных составляющих с учётом вида корней.

6. Определение тем или иным способом необходимых начальных условий.

7. Нахождение постоянных интегрирования из начальных условий.

8. Запись искомых величин в окончательной форме.