Тема 4. Ряды динамики

Рядом динамики называют расположенные в хронологическом порядке данные о развитии какого-либо явления во времени.

Состоит ряд динамики из двух элементов: временной компоненты, которая обозначается буквой "t" и уровня явления, обозначаемого "y".

Динамику явления характеризуют несколько показателей: абсолютный прирост, темп роста и темп прироста.

Обобщенную характеристику динамики получают при помощи средних показателей: среднего уровня ряда, среднего абсолютного прироста, среднего темпа роста и прироста.

Для того, чтобы определить характер и направление развития явления выявляют основную тенденцию его развития при помощи подходящего математического уравнения.

Кроме того, при наличии значительных сезонных колебаний рассчитывают индексы сезонности.

Для расчета первой группы показателей используются следующие формулы:

1. Абсолютный прирост (сокращение)

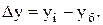(4.1)

2. Темп роста

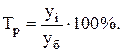(4.2)

3. Темп прироста

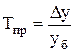, (4.3)

или Т_пр = Т_р -100%, (4.4)

где Δу - абсолютный прирост (сокращение);

у_i - сравниваемый уровень ряда;

у_б - уровень явления в периоде, принятом за базу сравнения;

Т_р - темп роста;

Т_пр - темп прироста.

Показатели динамики бывают цепными и базисными в зависимости от использования постоянной или переменной базы сравнения. Если в качестве базы сравнения используются уровни предшествующих периодов, такие показатели называются цепными. При использовании неизменной базы сравнения (как правило, первого уровня ряда динамики) рассчитывают базисные показатели динамики.

Расчет средних показателей в рядах динамики зависит от вида ряда.

1. В моментных рядах полных (у которых интервалы между временными компонентами равны) средний уровень определяется по формуле средней хронологической:

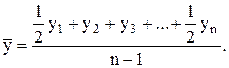(4.5)

2. В моментных рядах неполных (которых интервалы между временными компонентами различаются) средний уровень определяется по формуле средней арифметической взвешенной:

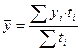. (4.6)

где t_i – период времени, в течение которого уровень явления не менялся.

3. В интервальных рядах средний уровень рассчитывается по средней арифметической простой:

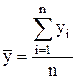. (4.7)

4. Средний абсолютный прирост:

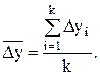(4.8)

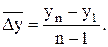или (4.9)

Формула (4.8) может быть использована только в полных рядах динамики.

5. Средний темп роста:

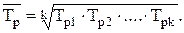(4.10)

или 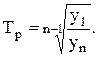(4.11)

Формула (4.10) может быть использована только в полных рядах динамики.

6. Средний темп прироста:

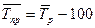, (4.12)

где у_i - уровень ряда в i-м периоде;

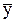- средний уровень ряда;

n - количество уровней в ряду динамики;

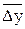- средний абсолютный прирост;

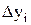- цепной абсолютный прирост в i-м периоде;

k - количество абсолютных приростов или темпов роста в изучаемом ряду динамики;

y_n - последний уровень ряда динамики;

T_p - темп роста;

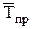- темп прироста средней;

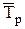- средний темп роста.

Если в ряду динамики необходимо выявить основную тенденцию развития, для этого подбирают подходящую математическую функцию и рассчитывают параметры соответствующего уравнения.

При использовании уравнения прямой 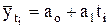расчет параметров производится по следующим формулам:

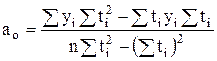, (4.13)

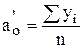; (4.14)

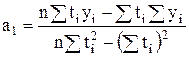, (4.15)

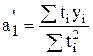, (4.17)

где у_i - реальные уровни ряда;

t_i - порядковые номера уровней ряда;

n - количество уровней;

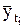- теоретические уровни ряда.

Формулы (4.13) и (4.14) применяются для упрощенных расчетов по методу отсчета от условного нуля. В этом случае уровни ряда (t) нумеруются таким образом, чтобы их сумма 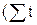) была равна нулю.

При использовании функции параболы второго порядка расчеты параметров при использовании метода отсчета от условного нуля осуществляются по формулам:

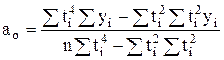, (4.18)

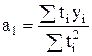; (4.19)

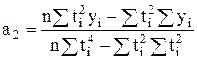. (4.20)

Уравнение в этом случае имеет вид:

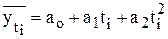. (4.21)

Для параболы третьего порядка использование метода отсчета от условного нуля дает следующие формулы параметров:

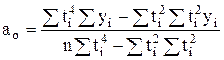, (4.22)

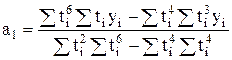, (4.23)

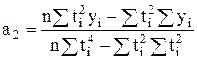, (4.24)

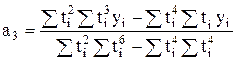. (4.25)

Уравнение параболы третьего порядка имеет вид:

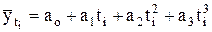. (4.26)

Для показательной функции 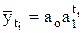(4.27)

расчет параметров уравнения (при 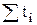= 0) осуществляется по следующим формулам:

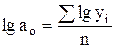, (4.28)

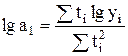. (4.29)

Если выравнивание осуществляют одновременно по нескольким уравнениям, наиболее подходящая функция выбирается на основе сравнения стандартизированных ошибок аппроксимации:

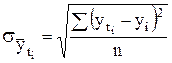. (4.30)

Для изучения сезонных колебаний в рядах динамики рассчитывают индексы сезонности. В общем виде индекс сезонности рассчитывается как отношение уровня явления в определенном сезоне к среднему годовому уровню явления:

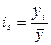. (4.31)

При наличии основной тенденции развития индекс сезонности рассчитывается на переменной базе сравнения, т.е. в качестве среднего уровня принимается эмпирический уровень явления. Вначале исчисляют индивидуальные индексы сезонности (4.31):

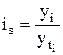. (4.32)

При наличии данных за несколько лет исчисляют средний индекс сезонности на основе индивидуальных индексов:

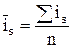, (4.33)

где y_i - реальные уровни ряда;

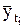- эмпирические уровни ряда, рассчитанные при помощи уравнений динамики;

n - количество лет;

i_s - индекс сезонности индивидуальный.

Если тенденция развития отсутствует, средние индексы сезонности исчисляются при помощи способа постоянной средней:

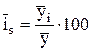, (4.34)

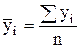, (4.35)

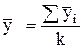, (4.36)

где 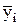- средние уровни одноименных внутригодовых периодов;

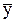- общая средняя уровней ряда за несколько лет;

n - количество лет;

k - количество внутригодовых периодов.

Для прогнозирования возможных уровней ряда в рядах динамики используется метод экстраполяции. Экстраполяцию можно осуществлять с использованием как средних абсолютных приростов, так и средних темпов роста. В первом случае формула примет вид:

, (4.37)

где y_n - последний известный уровень ряда динамики;

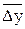- средний абсолютный прирост в анализируемом ряду динамики;

l - срок прогноза.

Используя для прогноза средний темп роста, перспективное значение определим следующим образом:

, (4.38)

где 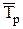- средний темп роста.