Компьютерное проектирование промывки скважин 2 страница

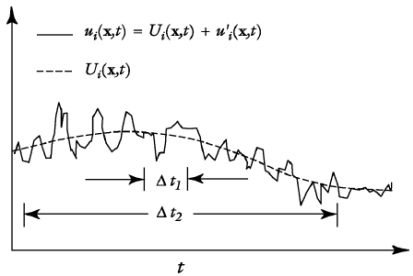
Рисунок 1.1 – Формализация фактического тренда фазовой переменной

нестационарного процесса турбулентного течения

На рисунке представлена типичная зависимость параметров процесса турбулентного течения от времени. В данном случае приведена зависимость для скорости, но аналогичный характер изменения имеют и другие параметры процесса, например, давление и вязкость. Как видно из рисунка, изменение параметров процесса турбулентного течения происходит в двух масштабах времени, причем зависимость средней скорости 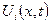достаточно гладкая и имеет периодический характер, что способствует ее математическому описанию. При этом мелкомасштабные колебания, определяющие величину , несмотря на кажущуюся хаотичность, достаточно закономерно колеблются относительно осредненной скорости, что предопределяет эффективность применения статистического инструментария их моделирования. Таким образом, если исходная зависимость представляется весьма сложной для моделирования, то покомпонентное моделирование не доставляет серьезных проблем, а получив модели каждого из компонентов, можно легко восстановить исходную зависимость с достаточно высокой точностью.

Точки 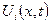получаются путем интегрирования в пределах интервалов , на которые разбивается исходная зависимость. Затем по полученным точкам находится непрерывная модель , используя которую вычисляют точки .

При решении системы RANS в трехмерном пространстве методом конечных элементов, за счет даже симметричного RST мы получаем шесть дополнительных уравнений для шести неизвестных, которыми являются составляющие скоростей флуктуации по осям координат. Однако решить, полученную таким образом систему, невозможно, так как в ней содержатся еще и статистические неизвестные, возникшие при моделировании. Из-за этих неизвестных система RANS не является замкнутой, что получило название – «проблема замыкания уравнений турбулентности» (the closure problem of turbulence).

Известно множество решений указанной проблемы, отличающихся допущениями и гипотезами относительно характера турбулентного потока. Так, например, на ранних этапах моделирования турбулентного потока энергия вихрей учитывалась за счет введения дополнительной вязкости, которая не зависела от координат и времени. Таким образом, изменение количества движения, происходящее в турбулентных вихрях, подменялось изменением вязкости жидкости в рамках модели параллельного сдвига, действующей при моделировании ламинарного потока. Иначе говоря, для моделирования турбулентного потока использовалась модель ламинарного потока, усовершенствованная путем увеличения вязкости жидкости на флуктуационную составляющую. Действующая при этом эквивалентная вязкость турбулентного потока, была названа «турбулентной вязкостью» (turbulent viscosity). Первоначально при моделировании использовалась турбулентная вязкость, не зависящая от координат и времени, которая в более поздних и развитых моделях была заменена функцией координат и фазовых переменных. Разновидностей функции турбулентной вязкости предложено достаточно много, поэтому классификация моделей турбулентного потока выполняется по формальному признаку количества уравнений, введенных в систему дополнительно к уравнениям движения и неразрывности.

На практике достаточно распространен 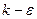метод замыкания системы RANS – « 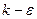closure», основанный на аналогии между хаотичным тепловым движением молекул газа и динамикой завихрений в турбулентном потоке. Данному методу соответствует функция турбулентной вязкости (), связывающая ее с отношением кинетической энергии турбулентного потока () к диссипации этой энергии (), посредством эмпирической константы 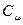=0,09

. (1.27)

При этом RST выражается через градиент скорости потока и турбулентную вязкость следующим образом

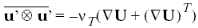. (1.28)

Подставляя выражение для RST в RANS, получаем основное уравнение движения, соответствующее математической модели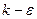

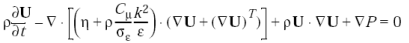, (1.29)

где – турбулентная энергия (м²/с²);

– диссипация (м²/с³).

Уравнение неразрывности потока в модели 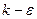не отличается от RANS

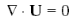. (1.30)

Поскольку в уравнении движения появились две новых статистических переменных, в систему дифференциальных уравнений модели 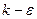добавляются два дополнительных уравнения, определяющие данные переменные.

Турбулентная энергия выражается уравнением, получаемым путем аналитических преобразований (1.28)

, (1.31)

а диссипация – преимущественно эмпирическим уравнением

,(1.32)

где 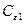=0,1256, =1,92, =1, 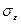=1,3 – эмпирические константы.

Таким образом, согласно принятой классификации, модель 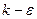относится к классу «турбулентных моделей двух уравнений» (two-equation models). Данный класс моделей характеризуется относительной простотой решения, так как количество дополнительных уравнений невелико, но также известно, что точность получаемых с их помощью решений невысока, хотя и приемлема для практических расчетов.

Известными случаями, когда модель 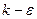работает с невысокой точностью, являются:

- расчет вращающихся потоков, например, поток бурового раствора в кольцевом пространстве скважины при вращении бурильной колонны;

- расчет в зонах рециркуляции, сопряженных с объемным расширением потока, например, когда буровой раствор попадает по трубопроводу в отстойник или амбар.

Тем не менее, для большого количества практических задач, включая расчет местных сопротивлений в циркуляционной системе буровой и скважине, расчет статических перемешивающих устройств в системе приготовления бурового раствора и расчет промывки кольцевого и внутритрубного пространств скважины при развитом турбулентном режиме, точность результатов моделирования достаточно высока.

В сравнении с моделями высоких классов, демонстрирующих большую достоверность результатов моделирования, основным достоинством модели 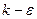является нетребовательность к вычислительным ресурсам, что обеспечивает решение задач на непрофессиональных компьютерах, работающих под управлением Windows с доступным объемом адресуемого пространства оперативной памяти до 4 Гб.

Вместе с тем, все вышеперечисленное относится к расчету сплошной, т.е. изотропной, среды, каковой является промывочная жидкость в основном объеме канала течения, тогда как в его пристенной зоне расчетная среда становится анизотропной. При этом степень анизотропии зависит от развитости турбулентности в потоке. Для получения результатов моделирования, согласующихся с практикой, анизотропию жидкости необходимо учитывать, что делается за счет использования специальных граничных условий, называемых «функциями стенки» (wall-function).

Существует две основных разновидности функций стенки. Первая разновидность основана на введении дополнительных составляющих в уравнение движения, характеризующих пристенный эффект. Необходимым условием применимости данного подхода является детализация расчетной сетки в зоне вблизи стенки для корректного моделирования, так называемого, ламинарного или вязкого подслоя (viscous sublayer). Степень необходимой детализации сетки определяется толщиной ламинарного подслоя, динамически изменяющейся вместе с интенсивностью потока, описываемой числом Рейнольдса. Таким образом, данная разновидность функций стенки обеспечивает наилучший результат при моделировании переходного потока или неразвитого турбулентного потока, существующего при невысоких числах Рейнольдса. Однако необходимость тонкой адаптации сетки делает программную реализацию функции стенки весьма сложной, что ухудшает сходимость алгоритма расчета в целом.

Вторая разновидность функций стенки опирается на существование эмпирически обоснованной взаимосвязи между скоростью жидкости и ее трением о стенку, локализованном в тонком пристенном слое. Данная разновидность функций стенки применяется для развитого турбулентного потока, когда толщина ламинарного подслоя настолько незначительна, что уже не определяет результат моделирования, т.е. когда имеет место режим граничного трения, а также когда изменения давления вдоль стенки достаточно малы. Тем не менее, успешное применение данной разновидности функций стенки возможно и при небольших числах Рейнольдса, при условии достаточного эмпирического обоснования, что делает ее наиболее универсальной.

Рассмотрим свойства функции стенки, основанной на граничном трении.

Прежде всего, отметим, что толщина граничного слоя, локализующего в себе трение, определяется отношением кинематической вязкости жидкости () к скорости скольжения (трения) (), называемым также «характеристической длиной» (relevant length scale)

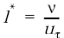, (1.33)

где 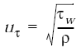; (1.34)

– напряжение сдвига жидкости по поверхности стенки;

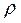– плотность жидкости.

На удалении от стенки много большем, нежели величина , параметры сплошного изотропного потока рассчитываются как функции координат с использованием модели турбулентного течения. В промежутке между граничным слоем и сплошным потоком находится буферная зона, в пределах которой действует универсальный закон распределения скоростей

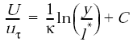, (1.35)

где 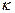– постоянная Кармана, равная 0,42;

С – постоянная, характеризующая шероховатость стенки, и равная 5 для гладкой поверхности;

– расстояние от стенки по нормали к ее поверхности.

Выражение под знаком натурального логарифма называется безразмерной или относительной координатой и обозначается

. (1.36)

Рассматривая равновесие между буферной зоной и граничным слоем, привлекая уравнения преобразования кинетической энергии потока в диссипацию, получаем выражение граничного условия стенки для модели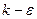

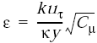. (1.37)

Учитывая также, что на стенке вектор потока для импульса эквивалентен напряжению сдвига, получаем

. (1.38)

Подставляя в полученное уравнение выражение для скорости скольжения, получаем граничные условия для и в следующем виде

, (1.39)

. (1.40)

Несмотря на кажущуюся простоту, полученные граничные условия не позволяют сразу вычислить значения и на стенке канала, ввиду того, что величина скорости скольжения – , зависящая от напряжения сдвига на стенке канала – 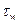, неизвестна до проведения расчета, так как определяется его результатами в виде следующей зависимости

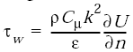, (1.41)

где – скорость течения жидкости вдоль стенки канала.

Данное обстоятельство накладывает ограничение на вид граничных условий, которые преобразуются в вырожденную форму (weak form) с целью введения в расчет тангенциального множителя Лангранжа – , с физической точки зрения соответствующего 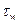. Поскольку для вычисления существуют надежные математические методы, его введением обеспечивается функционирование рассмотренной функции стенки.

Кроме того, заранее неизвестна толщина граничного слоя, характеризующаяся переменной , значение которой, тем не менее, должно быть задано до проведения расчета. На практике задается начальное приближение границы пристенного слоя, которое выбирается исходя из его попадания в диапазон , определенный эмпирически для случая сплошного граничного слоя.

Таким образом, решение задачи расчета турбулентного течения с использованием полуэмпирической модели 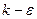опирается на ряд рекурсивных процедур, что предопределяет итеративный характер расчета, когда сначала при установленных начальных приближениях прямыми методами решается уравнение движения, т.е. находятся фазовые переменные u, v и p, затем решаются уравнения для и , на основе чего корректируются начальные приближения. Данная последовательность циклически повторяется до тех пор, пока изменение значений фазовых переменных в двух соседних петлях цикла не станет меньше предустановленного значения погрешности вычислений.

1.4 Методы решения уравнений, описывающих течение жидкостей

Приведенные выше уравнения относятся к классу дифференциальных уравнений в частных производных, универсальным методом решения которых, используемым в том числе и «FEMLAB», является метод конечных элементов (МКЭ). Суть МКЭ состоит в том, чтобы заменить истинное решение дифференциального уравнения, существующее на всей области определения, но известное лишь в некоторых ее точках, непрерывной аппроксимацией этого решения. При этом искомое решение, которое не выражалось в виде элементарных функций путем интегрирования исходного дифференциального уравнения или результатов его тождественных преобразований, выражается приближенно в аналитическом виде путем применения специальных численных методов аппроксимации данных. Проще говоря, когда решение уравнения настолько сложное, что не существует пригодной для его выражения элементарной функции, то это решение выражается в виде набора таких функций. Собственно, понятие МКЭ существует во взаимосвязи с определенной группой методов, предназначенных для отыскания набора функций и их комбинации, в совокупности представляющих решение дифференциального уравнения.

Один из методов, принадлежащих этой группе – это метод взвешенных невязок, суть которого состоит в следующем. Подбирается функция, удовлетворяющая дифференциальным уравнениям и краевым условиям, но подбирается не произвольно, поскольку такой подбор вряд ли возможен уже в двухмерном пространстве, а с использованием специальных методов.

Пусть состояние некоторой среды описывается дифференциальным оператором

LV+P=0, (1.42)

где L – дифференциальный оператор, например, оператор Лапласа;

V – фазовая переменная – неизвестная функция, которую следует найти;

P – величина, не зависящая от V.

Решение (1.42) выполняется совместно с граничным условием первого рода (Дирихле), то есть на границе задано значение фазовой переменной

V(Г)=V_Г . (1.43)

Решение ищется с помощью функции следующего вида

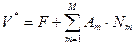, (1.44)

где V^* – приближенное решение;

F – функция, удовлетворяющая граничным условиям;

N_m – пробные функции, которые на границе области должны быть равны нулю;

A_m – неизвестные коэффициенты, которые необходимо отыскать из условия наилучшего удовлетворения дифференциальному оператору;

M – число пробных функций.

Если подставить V^* в исходный дифференциальный оператор (1.42), то получим невязку R=LV^*+P, изменяющуюся в области решения. Иначе говоря, в каждой точке решения невязка, т.е. его отличие от истинного значения, имеет свое значение.

При этом, поскольку цель – получить V^* максимально приближенное к истинному решению на всей области определения, то необходимо сформулировать условие, позволяющее минимизировать невязку в этой области. Одним из вариантов такого условия может быть следующее уравнение

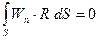, (1.45)

где W_n – весовые функции, в зависимости от выбора которых, различают варианты метода взвешенных невязок;

S – область пространства, в которой ищется решение.

При выборе в качестве весовых функций дельта-фукций будем иметь метод, который получил название «метод поточечной коллокации», для кусочно-постоянных функций – «метод коллокации по подобластям», но наиболее распространенным является «метод Галеркина», в котором в качестве весовых функций выбираются пробные функции N. В этом случае, если количество пробных и весовых функций равно, то после раскрытия определенных интегралов приходим к замкнутой системе алгебраических уравнений относительно коэффициентов A, которая в матричной форме записи имеет следующий вид

KA+Q=0. (1.46)

В (1.46):

- K – матрица, элементы которой рассчитываются по формуле

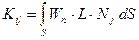; (1.47)

- Q – вектор, элементы которого рассчитываются по формуле

(1.48)

Решая (1.46) с учетом (1.47)-(1.48), находим вектор A, элементами которого являются искомые коэффициенты A_m. Подстановка найденных коэффициентов A_m в (1.44) дает решение исходной задачи.

Из вышеизложенного очевидны недостатки метода взвешенных невязок. Поскольку решение ищется сразу по всей области, то количество пробных и весовых функций должно быть значительным для обеспечения приемлемой точности. Однако при этом возникают трудности при вычислении коэффициентов K_ij и Q_i, связанные с необходимостью вычисления двойных и тройных интегралов по областям с криволинейными границами при решении плоских и объемных задач. Поэтому на практике метод взвешенных невязок не использовался, до изобретения метода конечных элементов. Идея последнего заключена в том, чтобы в методе взвешенных невязок воспользоваться простыми пробными и весовыми функциями, но не во всей области S, а ее отдельных подобластях (конечных элементах). При этом точность решения задачи обеспечивается использованием большого числа конечных элементов (КЭ), относительно простой формы, вычисление интегралов по которым не представляет сложности. Математически переход от метода взвешенных невязок к МКЭ осуществляется с использованием специальных пробных функций, называемых также «глобальными базисными функциями», которые обладают следующими свойствами:

- в узле аппроксимации функции имеют значение равное единице;

- отличны от нуля только в КЭ, содержащих этот узел аппроксимации, во всей остальной области равны нулю.

Для одномерной задачи набор таких кусочно-линейных функций, при количестве КЭ, равном трем, иллюстрируется рисунком 1.2.

На рисунке видно, что на каждом КЭ действует строго определенное число ненулевых глобальных базисных функций (в данном примере две), и вместо вычисления интеграла по всей области можно вычислить интегралы по КЭ и сложить их. Процедура сложения получила название «ансамблирование».

Рисунок 1.2 – Приближение решения пробными функциями в методе

конечных элементов

Использование глобальных базисных функций приводит к тому, что процедура вычисления интегралов по КЭ становиться достаточно простой и, поскольку в узлах аппроксимации N_m =1, коэффициенты A_m приобретают физический смысл, они становятся равными значению фазовой переменной в узлах. В аппроксимации (1.44) теперь можно отказаться от использования функции F, поскольку удовлетворить граничные условия можно естественным образом, задавая значения V в узлах, расположенных на границе.

В пределах одного КЭ, при условии, что он включен между i -м и j -м узлами, аппроксимацию решения можно определить с помощью глобальных базисных функций следующим образом

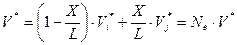, (1.49)

где X – текущая координата, отсчитываемая от начала КЭ;

L – его длина;

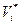и – значения фазовых переменных соответственно в i -ом и j -ом узлах КЭ.

Компоненты вектора N_e получили название «функций формы конечного элемента».

Функции формы можно получить и из других соображений. Зададимся полиномом, аппроксимирующим решение внутри конечного элемента, например

. (1.50)

Подстановка X =0 и X = L в (1.50) соответственно дает

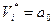, (1.51)

. (1.52)

Выражая из (1.51)-(1.52) коэффициенты a ₀ и a ₁, и подставляя их в (1.50), получаем

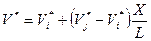, что эквивалентно (1.49).

Таким же образом, можно получить функции формы для квадратичной, кубической и других аппроксимаций. Соответственно аппроксимации называются и функции формы, а также КЭ – квадратичный, кубический и т.д.

Выбор конкретной аппроксимации зависит от нелинейности решаемой задачи – чем больше нелинейность V^*, тем более высокий порядок должна иметь принятая функция формы и соответственно КЭ. При этом действует следующее правило – порядок аппроксимирующего полинома должен быть больше или равен порядку решаемого дифференциального уравнения. Под порядком дифференциального уравнения понимается наибольший порядок производных, входящих в это уравнение.

Последовательность решения задач с использованием МКЭ приблизительно следующая:

а) выбирается вид КЭ;

б) строится сетка, т.е. область решения разбивается на КЭ;

в) определяется функция формы и математическая модель КЭ;

г) определяется математическая модель объекта путем ансамблирования;

д) задаются граничные условия;

е) решается полученная система алгебраических уравнений с получением в результате искомых коэффициентов, т.е. значений расчетных параметров (фазовых переменных) в узлах сетки.

На уровне пользователя из вышеперечисленного решаются следующие вопросы:

- выбор вида КЭ;

- задание параметров сетки;

- задание граничных условий.

Выбор вида КЭ тесно связан с выбором параметров сетки. Увеличение детализации сетки позволяет использовать более простые функции формы и наоборот. Поэтому нельзя говорить о выборе размера элемента или функции его формы независимо. Точно также в отношении этих параметров вряд ли употребим термин «правильный выбор»/ «неправильный выбор» – при решении задачи между ними всегда подбирается разумный баланс на основе нелинейности изменения фазовых переменных, сложности геометрии и наличествующих вычислительных ресурсов. Можно лишь говорить о путях подбора этого баланса, основанных на интерактивном взаимодействии пользователя с программой конечноэлементного анализа, используемой для решения.

1.5 Определение реологических параметров жидкостей

Адекватность гидравлических расчетов, выполняемых с привлечением зависимостей и методов компьютерного расчета, описанных в разделах 1.1-1.4, определяется корректностью используемых реологических параметров, включая вид реологической модели и входящие в нее скалярные коэффициенты. Прежде всего, следует понимать основное отличие компьютерного расчета, основанного на четких физико-математических выкладках и обоснованиях, от иных видов расчета, основанных полностью или частично на эмпирически обоснованных зависимостях. На эмпирическом уровне не составляет особого труда связать, например, перепад давления, возникающий при прокачке промывочной жидкости по участку циркуляционной системы с реологическими параметрами модели Бингама-Шведова, а затем сделать то же самое для модели Оствальда. При этом в обоих случаях будет обеспечиваться хорошее совпадение фактических потерь давления в скважине с потерями, предсказанными по уравнению, отображающую вышеупомянутую взаимосвязь, например, уравнению Дарси-Вейсбаха. Проблема в том, что корректность таких расчетов при переносе эмпирической взаимосвязи на другой участок скважины или иную систему технологической жидкости будет обеспечена лишь при условии совпадения методик определения реологических параметров и реологического поведения жидкости с принятыми при получении данной взаимосвязи. Для потери адекватности эмпирической взаимосвязи достаточно либо применить ротационный вискозиметр с другим рабочим зазором или иным характером поверхности измерительного цилиндра, либо буквально воспроизвести методику измерений на жидкости, отличающейся по своему реологическому состоянию. Это обусловлено тем, что при эмпирическом моделировании не учитываются детали процесса течения, так как взаимосвязь устанавливается на уровне макрофизических параметров системы, каковыми являются средняя скорость течения, расход, обобщенное число Рейнольдса и т.п.