Компьютерное проектирование промывки скважин 1 страница

КОМПЬЮТЕРНОЕ ПРОЕКТИРОВАНИЕ ПРОМЫВКИ СКВАЖИН

Учебно-методическое пособие

Уфа

Учебно-методическое пособие предназначено для изучения дисциплин «Компьютерное проектирование бурения скважин» и «Современные методы исследования, проектирования и обеспечения надежности нефтегазовых объектов» бакалавриатом и специалитетом направления 130500 «Нефтегазовое дело» профиля/специальности «Бурение нефтяных и газовых скважин».

Составитель: Соловьев А.Я., доц.

Рецензент: Исмаков Р.А., проф., д-р. техн. наук

© Уфимский государственный нефтяной технический университет, 2013

СОДЕРЖАНИЕ

Введение................................................................................................................................. 4

1 Методы компьютерного расчета течения жидкостей

1.1 Описание нестационарного потока несжимаемой жидкости...................................... 5

1.2 Описание спиралевидного потока несжимаемой жидкости........................................ 12

1.3 Описание турбулентного потока несжимаемой жидкости.......................................... 13

1.4 Методы решения уравнений, описывающих течение жидкостей.............................. 20

1.5 Определение реологических параметров жидкостей.................................................. 25

2 Основы работы в системе «FEMLAB»

2.1 Возможные постановки задач, модели и типы анализа.............................................. 32

2.2 Последовательность решения........................................................................................ 34

2.3 Построение сетки............................................................................................................ 35

2.4 Конфигурирование решателя......................................................................................... 40

3 Практикум

3.1 Расчет ламинарного установившегося течения в трубах............................................ 44

3.2 Расчет турбулентного течения в трубах....................................................................... 53

3.3 Расчет ламинарного установившегося течения в эксцентричном кольцевом пространстве....................................................................................................... 62

3.4 Исследование влияния вида реологической модели на параметры промывки эксцентричного кольцевого пространства скважины....................................................... 70

3.5 Оптимизация промывки эксцентричного кольцевого пространства скважины...................................................................................................... 74

Список литературы............................................................................................................. 79

ВВЕДЕНИЕ

Настоящее учебное пособие описывает возможности системы мультифизического моделирования «FEMLAB» версий 3.0-3.1 применительно к расчетам промывки скважин. Нынешнее название системы «FEMLAB» – это COMSOL Multiphysics – программный пакет, предназначенный для конечно-элементного анализа в различных областях физики и инженерного дела, включая рассмотрение связанных (мультифизических) задач. Возможности пакета освещены на сайте www.comsol.com. Среди областей его применения – механика конструкций, теплоперенос, инженерная химия (в том числе с учетом химической кинетики), электротехника, акустика, геофизика, связанные явления на микроуровне, оптические и высокочастотные эффекты. Уникальной чертой COMSOL Multiphysics является способность использовать аналитические возможности MATLAB. COMSOL Multiphysics обеспечивает эффективный обмен данными с популярными продуктами геометрического моделирования (Autodesk, Inventor, SolidWorks, CATIA, Pro/E, NX, SolidEdge и т.д.).

Из всего многообразия возможностей «FEMLAB» в пособии рассмотрено применение только одного модуля этой системы – Chemical Engineering Module ― совершенное средство анализа химических и связанных процессов. Этот модуль особенно удобен при рассмотрении процессов с одновременным учетом механики жидкостей и газов или транспортировки массы (энергии) и химической кинетики.

В первой части пособия рассмотрены уравнения математической физики, заложенные в программу, которыми определяются расчетные модели и расчетные схемы.

Во второй части освещены основные элементы интерфейса программы и приемы их использования.

В третьей части даны примеры решения практических задач, связанных с промывкой скважин.

Перечень задач, рассмотренных в пособии, не является исчерпывающим. Даны только те задачи, решение которых является базой для создания более совершенных моделей. Программа позволяет считать жидкости произвольной реологии, текущие в каналах сложной формы, поэтому ВУС, каверны, переходные потоки, вращающиеся колонны, турбулизаторы, амбары, отстойники, гидроциклоны – это все в ее возможностях. Как частный случай – фильтрация в пористых средах.

Модели, заложенные в программу, постоянно обновляются и совершенствуются. На сегодня применяется уже версия 4.3, возможности которой гораздо шире, но методология решения задач остается прежней.

1 МЕТОДЫ КОМПЬЮТЕРНОГО РАСЧЕТА ТЕЧЕНИЯ ЖИДКОСТЕЙ

1.1 Описание нестационарного потока несжимаемой жидкости

Если жидкость несжимаема, а ее вязкость постоянна, или изменениями плотности и вязкости жидкости допустимо пренебречь, то для расчета процесса ее течения применяется оригинальное уравнение Навье-Стокса [1, 2], основанное на законах сохранения импульса и энергии, выполняемых для каждой из составляющих вектора импульса по осям координат

. (1.1)

При необходимости учета изменений плотности жидкости, при условии их малости, а также возмущений вязкости, вызванных нестационарностью потока, для расчета течения ньютоновской жидкости используется обобщенное уравнение Навье-Стокса, модифицированное на основе аппроксимации Буссинеска

, (1.2)

где F – аппроксимация Буссинеска для объемных сил, таких как сила тяжести;

u – поле скоростей, в одномерном случае – вектор скорости в точке;

r – плотность жидкости;

h – динамическая вязкость жидкости;

p – давление.

Первое уравнение в системе (1.2) – это уравнение движения или сохранения импульса, тогда как второе – уравнение неразрывности. Если записать систему (1.2) в проекциях на координатные оси, то получим системы из трех и четырех уравнений для 2-D и 3-D размерностей задачи соответственно.

Выражение, стоящее под знаком дивергенции во втором члене левой части уравнения движения , называется тензором сил вязкости, поэтому система (1.2) получила также наименование вязко-тензорной формулировки (viscous stress tensor formulation). Данная формулировка накладывает ограничения на задаваемые граничные условия, не позволяя использовать в качестве таковых зависимости давления от координат, времени, скорости деформации, в том числе интегральные и дифференциальные. Эти ограничения затрудняют построение систем мультифизического моделирования, когда любая фазовая переменная может определяться решением другой системы дифференциальных уравнений, в свою очередь, зависящей от первой. Поэтому в системе «FEMLAB» применяется другая модификация обобщенного уравнения Навье-Стокса, называемая также обще-тензорной формулировкой (total stress tensor formulation)

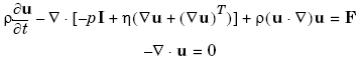, (1.3)

где – обобщенный тензор сил;

I – матрица идентичности (identity matrix).

Главным отличием обще-тензорной формулировки является наличие фазовой переменной – давления (p) под знаком дивергенции внутри тензора усилий, что позволяет учитывать при решении другие не объемные силы, возникающие помимо сил вязкости. Например, можно учитывать силы упругости или «эффект памяти», возникающий при течении полимерных растворов в скважине.

Переход от обобщенного тензора сил (s) к самому усилию (Т), приходящемуся на элементарную площадку, соответствующую ребру конечного элемента, производится по уравнению

, (1.4)

где n – вектор внешней нормали к анализируемому ребру (границе).

Получаемое таким образом усилие является обобщенным, т.е. включает все, действующие на ребро со стороны жидкости, силовые факторы. Из обобщенного усилия может быть выделена часть, обусловленная силами вязкости (K)

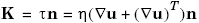. (1.5)

Таким образом, использованием (1.3) достигается возможность расчета течения нестационарных жидкостей. При этом следует обратить внимание на то, что нестационарность, учитываемая (1.3), может быть по вязкости (жидкости нестационарные по реологическому состоянию) или по давлению (вязко-упругие жидкости и жидкости с «эффектом памяти»), но не могут быть учтены значительные вариации плотности жидкости, так как они не входят в уравнение неразрывности. Допустимы только незначительные изменения плотности, например, возникающие под влиянием изменения температуры, которые учитываются свободной конвекцией, вводимой посредством аппроксимации Буссинеска в правую часть уравнения движения (1.3).

В случае неньютоновских жидкостей используется обобщенное уравнение Навье-Стокса для неньютоновских жидкостей, представляющее собой систему (1.2) или (1.3), дополненную реологическим уравнением состояния. В качестве последнего, как правило, задается зависимость эффективной вязкости жидкости от скорости сдвига, которая может вводиться в программу в произвольной форме, определяемой пользователем.

Предустановленными формами реологического уравнения состояния в «FEMLAB» являются:

- реологическое уравнение степенной жидкости, соответствующее степенному закону

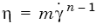, (1.6)

- реологическое уравнение, соответствующее модели Carreau

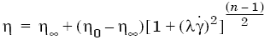, (1.7) где h – эффективная (кажущаяся) вязкость жидкости;

n – показатель нелинейности модели течения, характеризующий сдвиговое разжижение/загущение жидкости;

m – показатель консистенции жидкости, характеризующий ее прокачиваемость по скважине;

h_¥ – асимптотическая вязкость, определяемая как эффективная вязкость жидкости при бесконечно-большой скорости сдвига;

h₀ – предельная вязкость, определяемая как эффективная вязкость жидкости при нулевой скорости сдвига;

l – параметр Carreau, имеющий размерность времени и определяющий диапазон скоростей сдвига, где локализован перегиб на «S»-образной зависимости эффективной вязкости (реологической модели), а также направление перегиба;

g – скорость сдвига, определяемая как скорость скольжения элементарных слоев жидкости относительно друг друга, т.е. производная скорости течения по нормали к его оси.

Скорость сдвига в случае 3-D размерности модели рассчитывается по уравнению

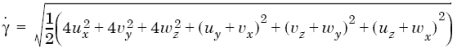, (1.8)

где u_x – производная составляющей скорости по оси –x;

u_y – производная составляющей скорости по оси –y;

w_z – производная составляющей скорости по оси –z.

Безотносительно конкретного вида реологического уравнения состояния, главной его характеристикой является непрерывность и положительная определенность при неотрицательных значениях скорости сдвига. Областью применимости реологических уравнений состояния являются не структурированные жидкости, в противном случае, для получения реологических параметров должны использоваться специальные методы, позволяющие избежать грубых ошибок, возникающих при неучете структурирования. В любом случае следует понимать, что расчеты по (1.2) или (1.3) основаны на постоянстве свойств сплошной среды в конкретной подобласти расчета, а динамическое структурообразование не согласуется с данным условием, в связи с чем оно может быть учтено только на уровне геометрии путем использования динамических границ. Поэтому в качестве реологического уравнения состояния не используются модели Гершеля или Бингама, так как они являются комбинацией свойств твердого тела и жидкости, что не позволяет корректно описывать свойства сплошной среды. Промежуточное положение между структурированными жидкостями, т.е. вязко-пластичными телами, и действительными вязкими жидкостями занимают полимерные системы, которые, вследствие наличия скольжения, имеют низкое предельное напряжение сдвига или, вообще, его не имеют, а также характеризуются постоянной эффективной вязкостью при скоростях сдвига менее 1 с^-1, называемой пластической вязкостью. Для описания движения таких систем лучше всего подходит модель Carreau, адекватно моделирующая участок реологической характеристики, лежащий в области проявления пластической вязкости, т.е. пластического режима течения.

Обобщенное уравнение Навье-Стокса также может быть записано в безразмерном виде

, (1.9)

где d – характеристическая длина, которая для случая течения в трубах равна гидравлическому диаметру;

u ₀ – характеристическая скорость, равная для того же случая средней скорости потока;

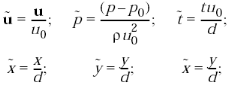
- величина обратная числу Рейнольдса;

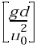- величина обратная числу Фруда.

Безразмерная формулировка обобщенного уравнения Навье-Стокса полезна для математического моделирования процессов течения жидкостей, которое позволяет получить решение для масштабной модели, а затем перенести его на натуру. Необходимость в моделировании возникает при расчете сложных объектов, когда прямой расчет в натурных условиях сложен или не осуществим, так как для этого требуется большое количество расчетных элементов, сложная мультиструктурная сетка, значительное количество системных ресурсов ПЭВМ. Применение моделирования позволяет совместить границы области расчета с геометрической сеткой, упростив, таким образом, форму расчетных элементов и уменьшив их количество, что в ряде случаев обеспечивает решение задач, неразрешимых в натурных условиях.

Поскольку уравнения, составляющие системы (1.2)-(1.3), дифференциальные, для их решения необходимы граничные условия, позволяющие определить константы интегрирования. Применительно к расчету ламинарного течения жидкостей, в системе мультифизического моделирования FEMLAB используются следующие граничные условия:

- Inflow/Outflow velocity – скорость на входе в расчетный элемент или выходе из него;

- Outflow/Pressure – давление на выходе из расчетного элемента при нестесненном истечении жидкости;

- Slip/Symmetry – ось потока;

- No slip – условие «прилипания» жидкости к стенке (не течет);

- Normal flow/Pressure – давление в живом сечении установившегося потока;

- Neutral – пассивная граница, которая не накладывает ограничений на вектор скорости, т.е. отсутствуют какие-либо взаимодействия жидкости с данной границей;

- Axial symmetry – ось симметрии.

Входная/выходная скорость задает составляющие скорости по осям координат во всех точках границы, соответствующей входному или выходному сечению расчетного элемента, что для 3-D размерности модели определяется уравнением

. (1.10)

Для двумерной модели в (1.10) отсутствует последняя составляющая, исключая случай расчета спиралевидного потока, когда в качестве данной составляющей используется скорость, направленная по касательной к окружности с центром на оси вращения потока.

Давление на выходе из расчетного элемента устанавливает значения удельных усилий, действующих по нормали к плоскости его выходного сечения, что в случае обще-тензорной формулировки дает

, (1.11)

где p ₀ – значение давления на выходе из расчетного элемента.

Из (1.11) явствует смысл условия нестесненного истечения жидкости, состоящий в том, что силы вязкости в выходном сечении не действуют, а помимо них обобщенный тензор усилий формируют только силы внешнего давления. Тогда в случае вязко-тензорной формулировки имеем

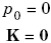. (1.12)

Сравнение (1.11) и (1.12) показывает, что граничное условие свободного истечения записывается в форме Неймана в случае обще-тензорной формулировки, и в форме Дирихле, когда используется вязко-тензорная формулировка. Таким образом, обще-тензорная формулировка является предпочтительной, так как позволяет в естественной форме задавать граничные условия по давлению, что необходимо при совместном решении систем дифференциальных уравнений в рамках мультифизического моделирования и физической связки с примыкающей подобластью расчета.

Ось потока предполагает равенство нулю производной по скорости, что в естественной форме может быть задано в виде двух ограничений. Первое – это равенство нулю нормальной, т.е. поперек оси течения, составляющей скорости

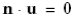. (1.13)

Второе – это отсутствие вязкого трения в окрестности оси потока, что соответствует нулевой тангенциальной составляющей тензора сил вязкости. Последнее условие для 2-D размерности модели эквивалентно

, (1.14)

а для 3-D размерности

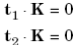, (1.15)

где t – орт, направленный вдоль оси потока.

Ось симметрии предполагает выполнение тех же уравнений (1.13)-(1.15), так как в случае осесимметричной модели, ось потока часто совпадает с осью симметрии, как, например, это имеет место в случае течения жидкости внутри труб. В противном случае, например, когда рассчитывается кольцевое пространство скважины, уравнения (1.13)-(1.15) теряют смысл, так как течение в районе оси симметрии не рассматривается. Тем не менее, задание оси симметрии в последнем случае необходимо для корректного вычисления поверхностных и объемных интегралов при интерпретации результатов расчета. При этом свойства сплошной среды в подобласти расчета, соответствующей внутритрубному пространству, не задаются, а сама эта подобласть деактивируется.

Условие «прилипания» означает, что скорости стенки и жидкости вблизи стенки равны. Для неподвижной стенки это дает

. (1.16)

Давление в сечении установившегося потока (условие стесненного входа/выхода) соответствует выполнению следующих уравнений в случае 2-D размерности модели и обще-тензорной формулировки

. (1.17)

Первое уравнение возникает по определению установившегося потока, как ламинарного относительного сдвига элементарных слоев, откуда следует равенство нулю тангенциальной, т.е. направленной вдоль плоскости сечения перпендикулярно оси потока, составляющей скорости.

Второе уравнение задает давление, аналогично условию нестесненного выхода (1.11).

В случае 3-D размерности модели, (1.17) преобразуется к виду

. (1.18)

Для вязко-тензорной формулировки вместо (1.17) получим

, (1.19)

а вместо (1.18)

. (1.20)

При задании геометрии области расчета часто возникают границы, которые не сопряжены с какими-либо специфическими физическими условиями, а служат лишь соединительным звеном между физически-обусловленными границами, позволяющим получить непрерывную расчетную область. Специально для таких границ предназначено условие пассивной границы, означающее, что в зависимости от формулировки, либо обобщенный тензор сил – для обще-тензорной формулировки, либо тензор сил вязкости – для вязко-тензорной формулировки, для данной границы равен нулю

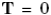, . (1.21)

Таким образом, пассивная граница не накладывает ограничений на поле скоростей, предполагая отсутствие взаимодействий между жидкостью и стенкой, т.е. с формальной физической точки зрения границы нет.

1.2 Описание спиралевидного потока несжимаемой жидкости

Значительная часть задач гидродинамики бурения скважин связана с закрученными или спиралевидными потоками («swirl flow»), возникающими при вращении бурильной колонны в скважине, а также использовании турбулизаторов, вихревых кольмататоров и т.д. Принципиальным отличием спиралевидного потока является наличие окружной составляющей скорости, направленной по касательной к окружности, полученной поперечным сечением внешней стенки бурильной колонны. В случае трехмерного моделирования обычного не спиралевидного потока вектор скорости в конкретной точке области расчета определяется тремя составляющими в соответствии с числом координатных осей

. (1.22)

Использование (1.22) при расчете спиралевидного потока сопряжено с рядом трудностей, так как направление окружной скорости не совпадает ни с одной координатной осью и, более того, в каждой точке окружности внешней образующей поперечного сечения колонны вектор окружной скорости находится под своим углом к координатным осям. Данное обстоятельство делает невозможным непосредственное задание физических свойств границы, соответствующей внешней стенке бурильной колонны, при использовании (1.22). В этой связи, в уравнение Навье-Стокса вместо фазовой переменной скорости вводятся:

- «вихревая функция» – y (stream function), для плоской задачи определяемая уравнением

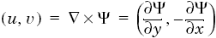; (1.23)

- «завихренность потока» – w, определяемая для тех же условий уравнением

. (1.24)

После преобразований получаем уравнение Навье-Стокса в «бездивергентном» виде

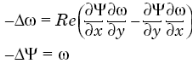. (1.25)

Заметим, что уравнение неразрывности в полученной системе отсутствует, а задача решается только в 2-D-Axial symmetry постановке.

1.3 Описание турбулентного потока несжимаемой жидкости

Физически- и математически-обоснованным расчетным уравнением движения жидкости в турбулентном режиме остается, рассмотренное выше, уравнение Навье-Стокса, которое применялось с соответствующей целью на ранних стадиях развития численного моделирования данного процесса. Однако главным недостатком этого метода решения задачи описания турбулентного течения жидкости является необходимость использования большого количества конечных элементов с целью корректного описания флуктуаций физических параметров в зонах турбулентных вихрей. Данное обстоятельство делает модели, основанные на прямом решении уравнения Навье-Стокса, малопригодными для практических расчетов турбулентного режима течения.

Способом преодоления указанной проблемы является ввод в систему расчетных уравнений статистических неизвестных. Таким образом, вместо аналитически строгих уравнений движения и непрерывности, составляющих систему уравнений Навье-Стокса, приходим к полуэмпирической системе уравнений, основанной на осредненных физических параметрах, вычисляемых в предположении, что изменение этих параметров – статистическая закономерность.

Примером такой модели является, так называемое, усредненное по Рейнольдсу уравнение Навье-Стокса – Reynolds Averaged Navier-Stokes (RANS):

, (1.26)

где – плотность жидкости (кг/м³);

– средняя скорость течения (м/с);

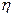– динамическая вязкость (Па*с);

– давление (Па).

Сравнение RANS с оригинальным уравнением Навье-Стокса (1.1) показывает, что отличием является последний член в левой части уравнения движения 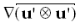, называемый силовым тензором Рейнольдса – Reynolds Stress Tensor (RST), который описывает возмущения скорости жидкости вокруг среднего значения. Теоретической базой, на которую опирается RST, является представление фазовой переменной турбулентного потока (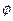), зависящей от времени и координат, в виде сумы среднего значения (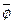) и флуктуационной части (). Схема, поясняющая данное разложение, представлена на рисунке 1.1.