Оригиналы с рациональными изображениями

При решении ряда важных задач очень часто приходится меть дело с дробно-рациональными функциями, то есть с функциями , где и – многочлены.

Дробно-рациональная функция называется правильной, если степень знаменателя больше степени числителя .

Теорема 2.4. Всякая правильная дробно-рациональная функция является изображением.

Доказательство. Пусть – правильная дробно-рациональная функция. В разделе об интегрировании правильных рациональных дробей была доказана теорема о разложении дробно-рациональной функции на сумму элементарных дробей. Поэтому функцию мы можем представить в виде суммы дробей следующего вида:

, , , , ,

где 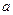и – вещественные числа.

Из формул , , 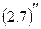(2.15) и (2.4) немедленно следует, что каждая из функций , , является изображением

,

.

.

Покажем, что функция , также является изображением. Действительно, пусть сначала к = 2, тогда

.

Так как каждая из функций и 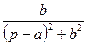, как показано выше, является изображением, то и произведение двух изображений снова изображение (смотрите теорему о свертке), поэтому функция –изображение

Если к = 3, то

,

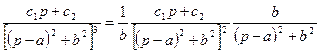но каждый из сомножителей как показано выше, является изображением, следовательно, и их произведение тоже изображение.

Переходя таким же способом от случая к = 3 к к = 4, от к = 4 к к = 5 и так далее, мы устанавливаем, что при любом к функция является изображением.

Таким образом, функция представляется суммой дробей, каждая из которых является изображением, следовательно, и сама является изображением, что и требовалось доказать.

Теорема 2.5. Дробно-рациональная функция , степень числителя которой меньше степени знаменателя имеющего корни 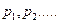, 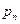кратностей , , является изображением функции 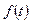, определяемой по формуле

. (2.22)
Выводы этой теоремы мы также примем без доказательства.

Следствие. Если все корни знаменателя дробно-рациональной функции простые, то есть , то по формуле вычета в простом полюсе

оригинал

. (2.23)

Пример 15. Найти оригинал для изображения .

По формуле (2.22) имеем

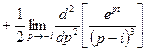
или, после дифференцирования и, переходя к пределу, получим

.

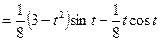Пример 16. Найти оригинал для изображения .

Здесь знаменатель имеет только простые корни 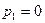, , 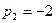, 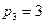поэтому применима формула (2.23). Так как здесь

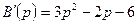
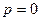
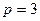
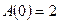
то по формуле (2.23) получаем

.