Скорость точки. Ускорение точки. Равнопеременное движение точки

Скорость точки

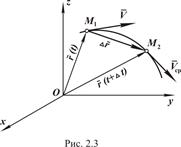
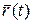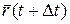Определим скорость точки, рассматривая векторный способ задания ее движения. Пусть в момент времени t положение точки определяется радиусом , а в момент ()  радиус-вектором . Вектор 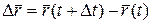есть вектор перемещения точки за время t (рис. 2.3).

Вводим понятие средней скорости, 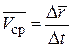. (2.3)

Скорость точки в данный момент времени есть предел отношения вектора перемещения 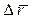к промежутку времени 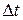, за который произошло это перемещение при 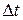, стремящемся к нулю, то есть

а это есть производная 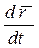. Таким образом, скорость точки равна производной радиус-вектора точки по времени, а именно 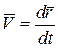, (2.4)

и направлена по касательной к траектории в сторону движения. Единицами измерения скорости являются м/c, км/ч.

Определение скорости
при координатном способе задания движения

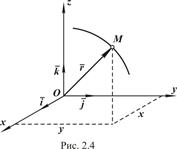Пусть движение точки задано в декартовой системе координат, являющейся неподвижной (рис. 2.4), то есть заданы координаты точки как функции времени x=x (t), y=y (t), z=z (t).

Используя единичные векторы 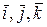осей x, y, z, определяем радиус-вектор: 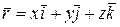(2.5)

и далее вектор скорости: 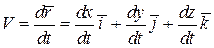, (2.6)

так как единичные векторы данной неподвижной системы координат постоянны.

Вектор скорости 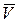, как и любой вектор, можно также представить через его проекции, используя единичные векторы, то есть .

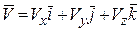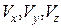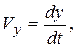
Сравнивая два последних выражения, получаем, что проекции скорости на координатные оси будут равны 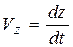, (2.7)

то есть проекция скорости точки на координатную ось равна первой производной по времени от соответствующей этой оси координаты.

Производную по времени в теоретической механике обозначают точкой сверху, поэтому можно еще записать 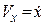, , 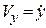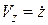. (2.8)

Вектор скорости определяется модулем 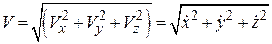(2.9)

и направлением, которое задается направляющими косинусами:

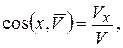
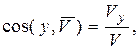
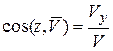. (2.10)

Определение скорости
при естественном способе задания движения

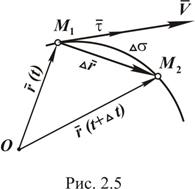
Пусть точка М движется по некоторой кривой (рис. 2.5). За промежуток времени t точка перемещается из положения 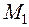в положение 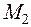по дуге.

Дуга обозначается как 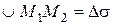, а перемещение – 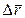. Зная, что ,

запишем его в другом виде:

.

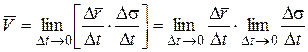Так как предел отношения дуги к стягивающей ее хорде равен по модулю единице, а предельное положение секуще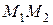й (при ) совпадает с направлением касательной к кривой в точке 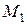, то ,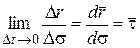

где 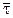 единичный вектор касательной к кривой, направленный в сторону положительного отсчета дуги (рис. 2.5).

Рассматривая второй предел 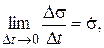получаем . (2.11)

Обозначив 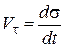, имеем , где 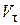 проекция скорости на касательную.

Ускорение точки

Определение ускорения точки при векторном способе задания движения. Полагаем, что в момент времени t скорость равна 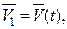а в момент времени 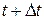– соответственно 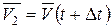(см.рис. 2.6).

Изменение вектора скорости за промежуток времени 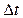определяется как

.

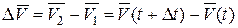Среднее ускорение определяем как отношение к 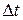, то есть .

Ускорение точки в данный момент времени есть предел отношения приращения скорости 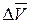к приращению времен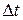и при 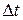, стремящемся к нулю: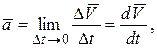

и так как 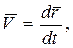то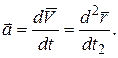

Следовательно, ускорение точки равно первой производной по времени вектора скорости точки или второй производной по времени радиуса-вектора точки. Единицей измерения ускорения является м/с .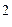

Определение ускорения при координатном способе задания движения. Пусть движение точки задано в прямоугольной системе координат:

x = x (t), y = y (t), z = z (t).

Ускорение точки определяется (2.13) как .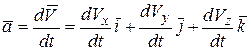

Вектор ускорения можно представить через его проекции .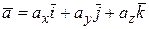

Сравнивая два последних выражения, имеем 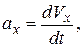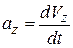, (2.14)

то есть проекция ускорения точки на какую-либо координатную ось равна первой производной от соответствующей проекции скорости.

Выражение (2.14), с учетом (2.8), можно представить в виде , , .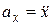

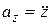Таким образом, проекция ускорения точки на какую-либо ось равна второй производной по времени от соответствующей координаты.

Модуль ускорения определяется как ,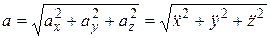

а направление задается направляющими косинусами: .

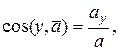
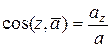Формулы (2.16), (2.17) полностью определяют вектор ускорения.

Определение ускорения при естественном способе задания движения. Прежде чем определить ускорение, введем некоторые понятия из дифференциальной геометрии. В каждой точке кривой можно указать три взаимно перпендикулярных направления – касательная, нормаль и бинормаль. Принимая эти направления за координатные оси, введем единичные векторы этих осей  .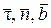

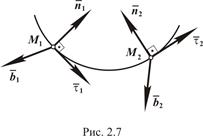Единичный вектор касательной 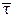уже был введен. Единичный вектор нормали 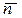направляем в сторону вогнутости кривой (рис. 2.7). Единичный вектор бинормали 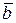направлен таким образом, чтобы единичные вектора 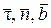образовывали правую систему координат.

Векторы 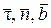являются единичными векторами осей естественного трехгранника.

Согласно выражению (2.13) ускорение точки , а ее скорость , следовательно,

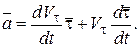
Примем без доказательства, что ,

где 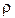 радиус кривизны траектории в рассматриваемой точке.

Отсюда имеем .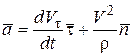

Видно, что ускорение имеет две составляющие: 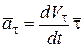и ,

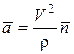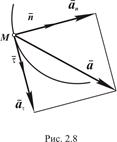направленные по 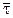и 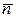(рис. 2.8), первая из которых называется касательным ускорением, вторая  нормальным ускорением.

Касательное ускорение характеризует изменение модуля скорости, а нормальное ускорение характеризует изменение скорости по направлению.

Модуль ускорения равен .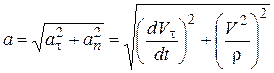

Составляющие ускорения всегда взаимно перпендикулярны (рис. 2.8).

Касательное ускорение равно нулю при движении точки с постоянной по модулю скоростью. Нормальное ускорение равно нулю при прямолинейном движении точки.